I’ve run into subsumption architectures a few times now. They’re basically a way to structure a complicated decision-making system by letting higher-level reasoning modules control lower-level reasoning modules. Recently, I’ve been thinking about some parallels there with the transformer architecture that has dominated large-scale deep learning. This article is a brief overview of subsumption architectures and attempts to tie them in with attention models, with the hope to better understand both.
What is a Subsumption Architecture?
The Wikipedia entry on subsumption architecture describes it as an approach to robotics from the 80s and 90s that composes behavior into hierarchical modules. The modules operate in parallel, with higher-level modules providing inputs to lower-level modules, thereby being able to operate and reason at a higher level.
These architectures were introduced by Rodney Brooks (of Baxter fame, though also much more) and his colleagues in the 80s. Apparently he “started creating robots based on a different notion of intelligence, resembling unconscious mind processes”. Brooks argued that rather than having a monolithic symbolic reasoner that could deduce what to do for the system as a whole, a subsumption approach could allow each module to be tied closer to the inputs and outputs that it cared about, and thus conduct local reasoning. This argument is often tied together with his view that, rather than making a big symbolic model of the world, which is a hopeless endeavor, that “the world is its own best model” and submodules should be able to directly interact with the portion of the world they interact with.
Perhaps this is best described using an example. Consider a control system for a fixed-wing aircraft. A basic software engineering approach might architect the aircraft’s code to look something like this:

where, for most flight dynamics, . Unfortunately, we run into some complexity as we consider the behavior of the longitudinal controller. When taking off, we want full throttle and to maintain a fixed target pitch, when flying below our target altitude, we want to use full throttle and regulate airspeed with pitch control, when near our target altitude we want to control our altitude with pitch and control our airspeed with throttle, and when above our target altitude we want zero throttle and to regulate airspeed with pitch control:
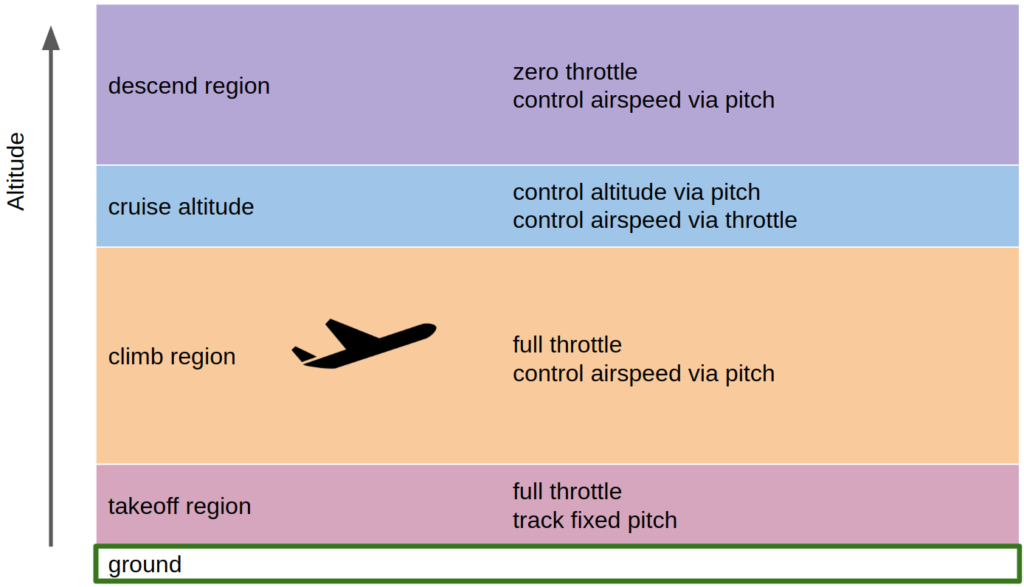
As such, our longitudinal controller has quite a lot of internal complexity! Note that this is only for takeoff to cruise; landing would involve more logic. We want to control our aircraft with different strategies depending on the context.
Subsumption architectures are a means of tackling this sort of context-based control. Rather than programming a bunch of if/then statements in a single longitudinal control module, we can further break apart our controller and allow independent modules to operate concurrently, taking control when needed:
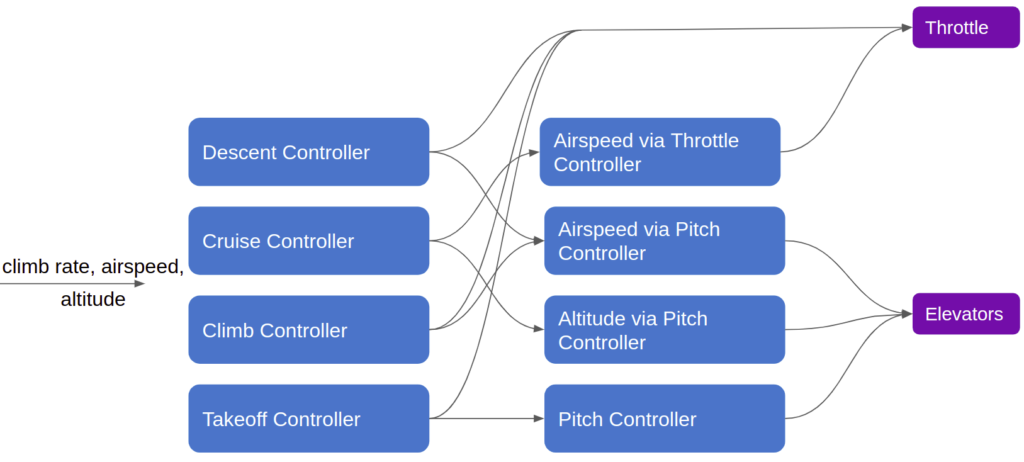
This architecture works by splitting our monolithic logic into independent modules. Each module can receive inputs from any number of upstream modules. For example, the throttle output module, which forwards the final throttle command to the motor, can receive direct throttle commands from the airspeed-via-throttle-controller, the descent controller, the climb controller, or the takeoff controller.
Each module thus needs a method for knowing which input to follow. There are multiple ways to achieve this, but the simplest is to assign different modules different priorities, and their outputs inherit those priorities. The highest propriety input into any given model would be the one acted upon. In our little example above, the cruise controller could just be running continuously, with its output being overwritten by the takeoff controller when it activates during takeoff.
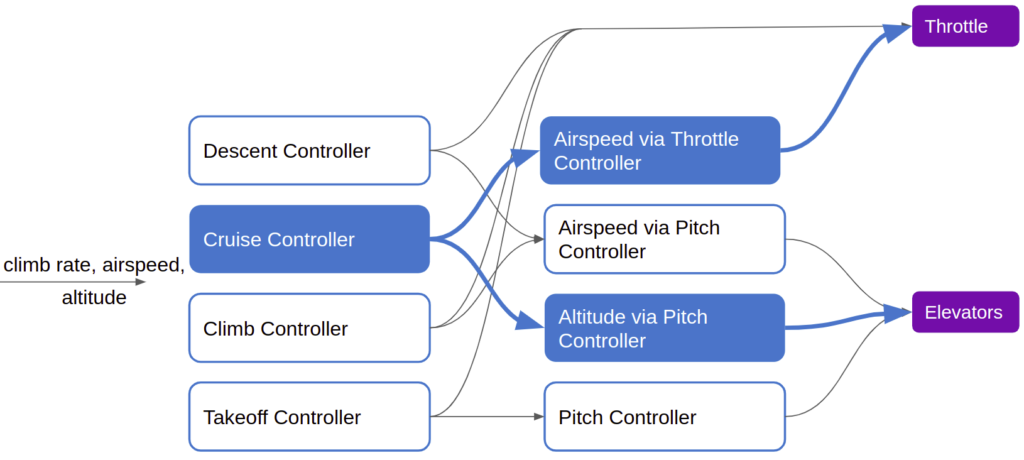
We get our emergent takeoff behavior by allowing the takeoff controller, when it activates, to override the cruise controller’s output:
This modularization has some major advantages. First, modules are self-contained, and it is much easier to define their desired behavior and to test it. It is much easier to validate the behavior of a simple pitch controller than the complicated behavior of the monolithic longitudinal controller. Second, the self-contained nature means that it is much easier to extend behavior by swapping or implementing new modules. Good luck having a new member of the team hook up everything properly in a monolithic code base.
We can similarly take this approach further and take it farther up the stack, with our longitudinal and lateral controllers taking inputs from trajectory trackers, or waypoint followers, a loitering controller, or a collision-avoidance module. All of the same principles apply. Finally, it is easier to monitor and debug the behavior of a modular system, especially if we make the modules as stateless as possible. We can log their inputs and outputs, and then can (more) easily figure out what the system was doing at any given time.
The approach is not without its disadvantages. The most obvious change is that we now have a bunch of disparate modules that can all act at various times. In the monolithic case we can often guarantee (with if statements) that only certain modules are active at certain times, and curtail complexity that way. Another issue is added complexity in handoff – how do we handle the transitions between module activations? We don’t want big control discontinuities. Finally, we have the issue of choosing priority levels. For simple systems it may be possible to have a strict priority ordering, but in more complicated situations the relative ordering becomes trickier.
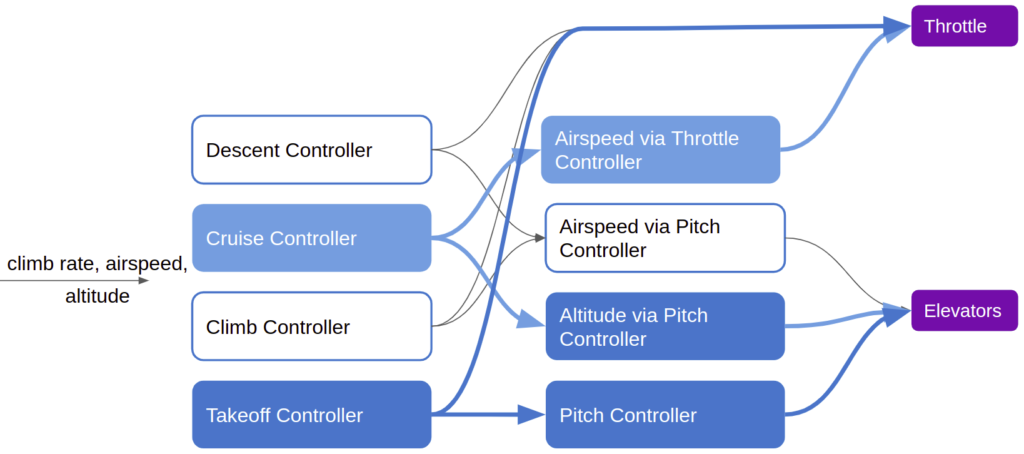
Subsumption architectures were originally invented to be able to easily introduce new behaviors to a robotic system. Our previous controller, for example, could be extended with multiple higher-level modules that use the same architectural approach to command the lower-level modules:
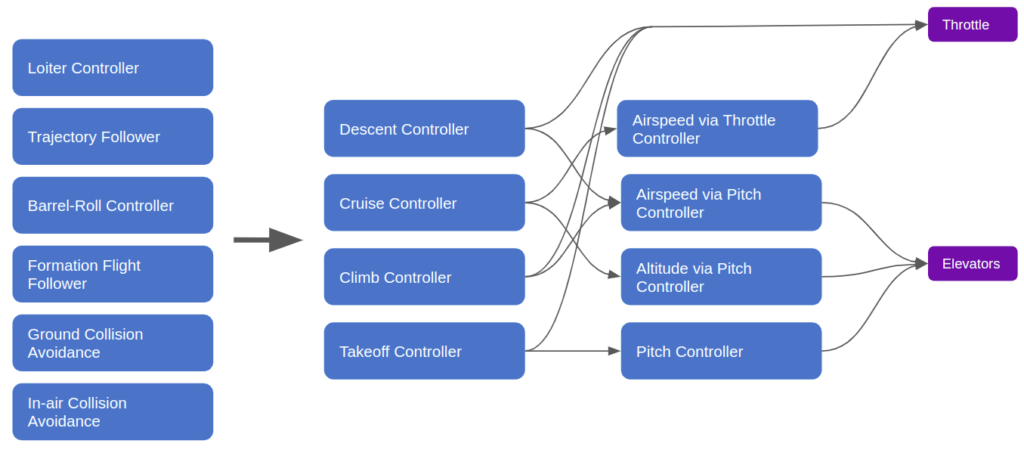
The running example is for a fixed-wing controller, but you could imagine the same approach being applied to a robot. The Wikipedia article suggests a higher-level exploration behavior that can call lower-level walk-around or avoid-object modules.
Unconscious Mind Processes
Brooks was originally motivated by subsumption architectures because it allowed for “unconscious mind processes”. By this I think Brooks meant that higher level controllers typically need not concern themselves with low level details, and could instead rely on lower level controllers to handle those details for them. In our example above, a trajectory follower can just direct the cruise controller to follow the trajectory, and does not need to think about elevator or throttle rates directly.
One might argue that claiming that this sort of an approach resembles how the human mind works is a stretch. We are all familiar with sensational articles making big claims on AI approaches. However, I think there are core ideas here that are in line with how human reasoning might come to be.
For example, Brooks argues that subsumption models have emergence. We don’t think of any of the lower-level modules as being particularly intelligent. A pitch controller is just a PID loop. However, the combined behavior of the symphony of higher-level modules knowing when to jump in and guide behavior causes the overall system to exhibit quite sophisticated reasoning. You, a human, also have some “dumb” low-level behavior – for example what happens when you put your hand on a hot stove top. Your higher-level reasoning can choose to think at the level of individual finger movements, but more often thinks about higher-level behavior like picking up a cup or how far you want to throw a baseball.
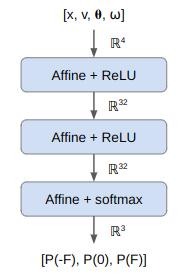
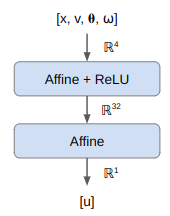
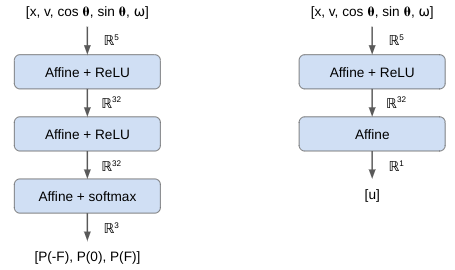
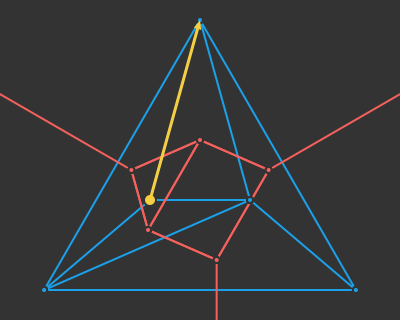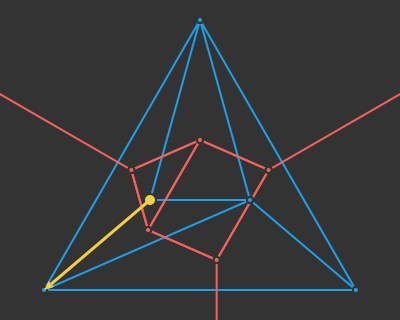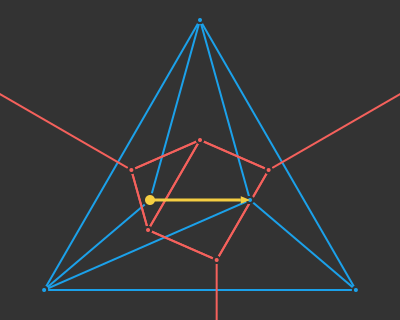
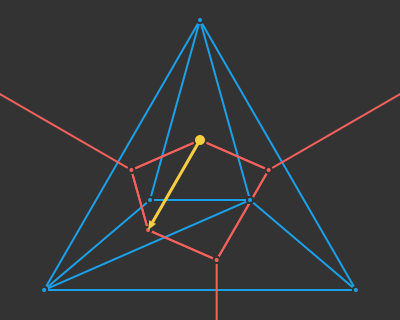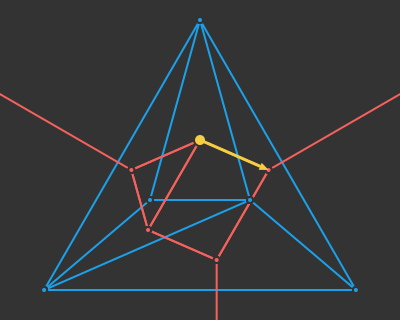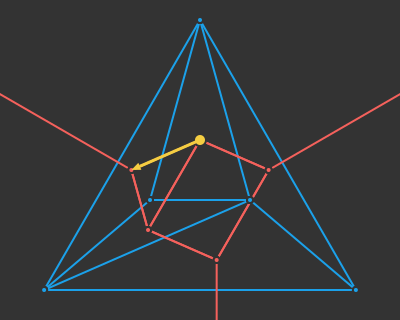
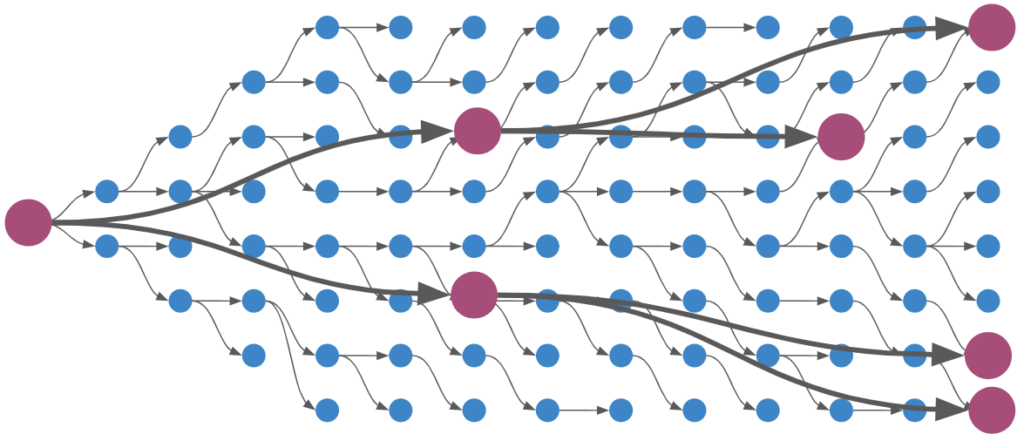
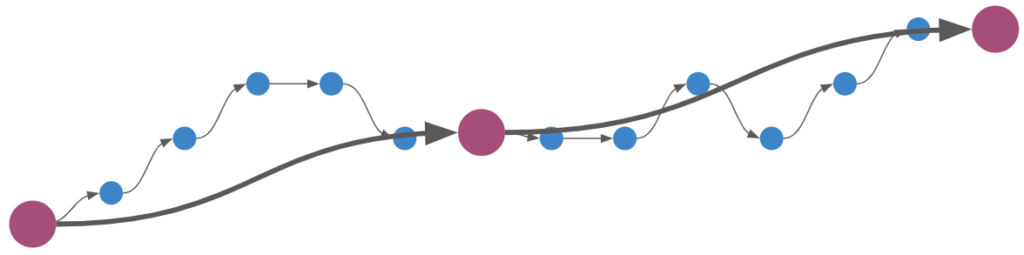
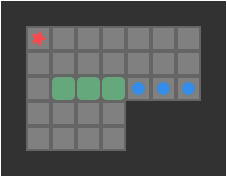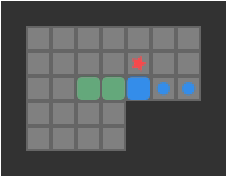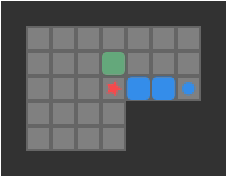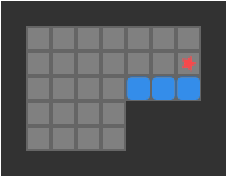
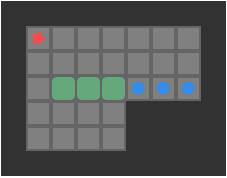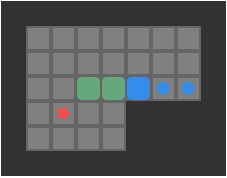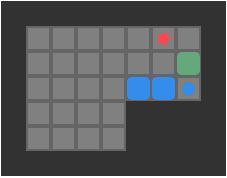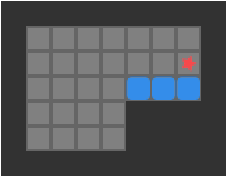
I think this line of reasoning bears more fruit when we consider the progress we have made with deep learning architectures. The field has more or less converged on a unified architecture – the transformer. Transformers depart from prior sequence learning architectures by doing away with explicit recurrence and convolution layers in favor of attention. Attention, it just so happens, is the process of deciding which of a set of inputs to pay attention to. Subsumption architectures are also very much about deciding which of a set of inputs to pay attention to.
We could restructure our subsumption architecture to use attention:
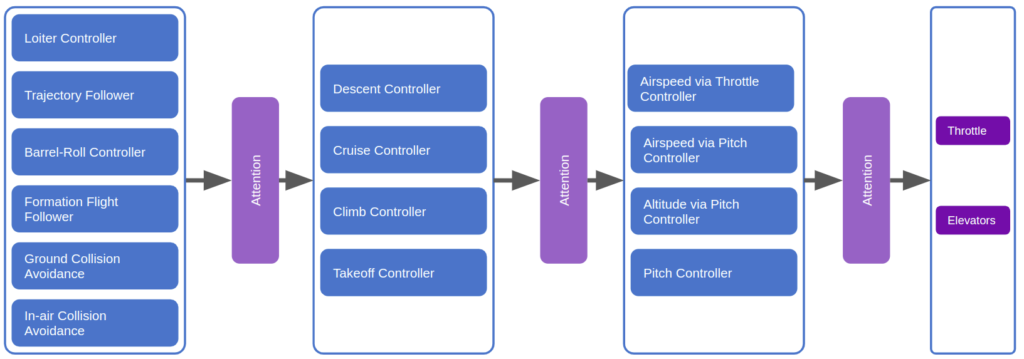
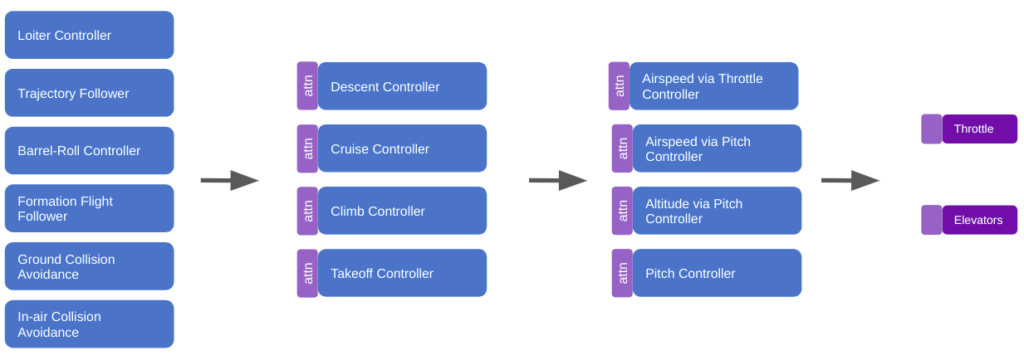
It would make a lot of sense for a robust deep learning model to have produced, inside of its layers, a diverse set of modules that can spring into action at appropriate moments and make use of other modules in lower levels. Such an outcome would have big wins in robustness (because lower-level modules become general tools used by higher-level modules), have the benefit of progressive learning (we’d refine our basic behaviors first, like when a child first learns how to walk before reasoning about where to walk to), and we’d be able to develop more nuanced behaviors later in life by building new higher-level modules.
Interestingly, this sort of emergence is the opposite of what a classical deep neural network typically produces. For perception, it has been shown that the first layers of a neural network produce high level features like edge detectors, and then the deeper you go, the more complicated the features get. Eventually, at the deepest levels, these neural networks have features for dogs or cats or faces or tails. For the subsumption architecture, the highest fidelity reasoning happens closest to the output, and the most abstract reasoning happens furthest from the output.
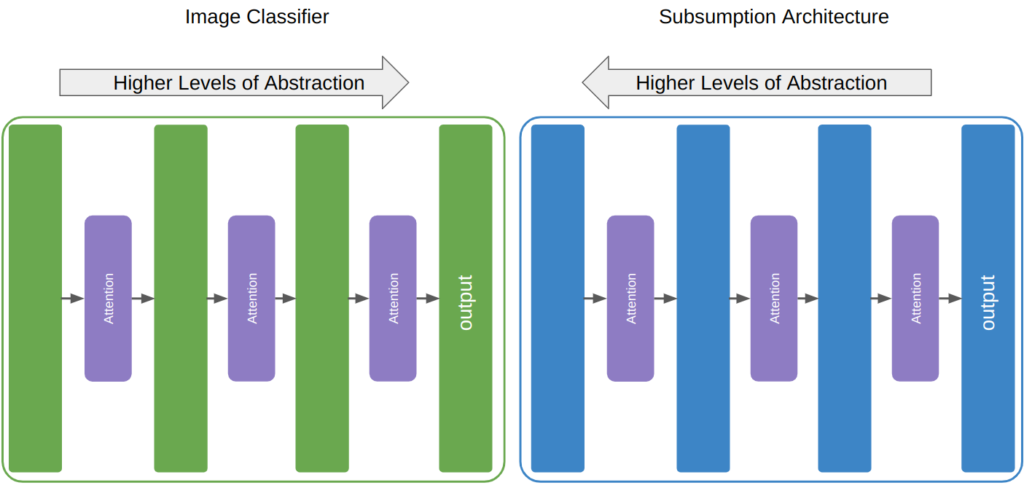
The Tribulations of Learning
Unfortunately, the deep-learning view of things runs into a critical issue – our current reliance on gradient information to refine our models.
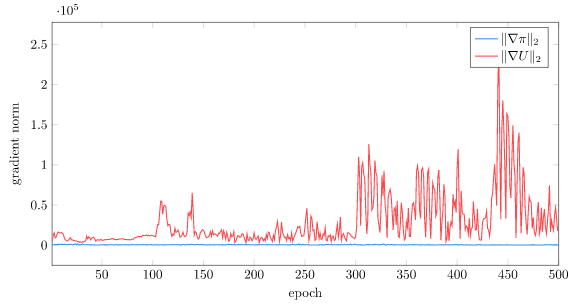
First off, the way we have things structured now requires gradient information from the output (i.e., motor controllers) to propagate back up the system to whichever cause produced it. That works pretty well for the modules closest to the output, but modules further from the output can suffer from vanishing gradients.
Vanishing gradients affect any large model. Modern architectures include skip connections (a la ResNet) to help mitigate this effect. It helps some.
Second, these models are typically trained with reinforcement learning, and more specifically, with policy gradient methods. These are notorious for being high variance. It can take a very long time for large-scale systems to learn to generalize well. Apparently Alpha Go played 4.9 million times in order to train itself to play well, which is way more than any human master ever played. Less structured tasks, like robot grasping, seem to also require massive quantities of training time and data.
This second problem is more or less the main stickler of reinforcement learning. We know how to build big systems and train them if we are willing and able to burn a whole lot of cash to do so. But we haven’t figured out how to do it efficiently. We don’t even know how to leverage some sort of general pre-training. There are certainly projects that attempt this, it just isn’t there yet.
The third problem is more specific to the hierarchical module architecture. If we get sparse activation, where some modules are only affected by certain parent modules, then there are presumably a bunch of modules that currently do not contribute to the output at all. The back-propagated gradient to any inactive module will be zero. That is bad, because a module with zero gradient will not learn (and may degrade, if we have a regression term).

I think the path forward is to find a way past these three problems. I suspect that subsumption architectures have untapped potential in the space of reinforcement learning, and that these problems can be overcome. (Human babies learn pretty quickly, after all). There is something elegant about learning reliable lower-level modules that can be used by new higher level modules. That just seems like the way we’ll end up getting transfer learning and generalizable reasoning. We just need a way to get rewards from places other than our end-of-the-line control outputs.
Conclusion
So we talked about subsumption architectures, that’s cool. What did we really learn? Well, I hope that you can see the parallel that we drew between the subsumption architectures and transformers. Transformers have rapidly taken over all of large-scale deep learning, so they are something to pay attention to. If there are parallels to draw from them to a robotics architecture, then maybe that robotics architecture is worth paying attention to as well.
We also covered some of the primary pitfalls. These challenges more or less generally need to be overcome to figure out scalable / practical reinforcement learning, at least practical enough to actually apply to complex problems. I don’t provide specific suggestions here, but oftentimes laying out the problem helps us get a better perspective in actually solving it. I remain hopeful that we’ll figure it out.