I spent a good while translating portions of the YASS Pascal code into Julia. I wanted to see how a larger, more sophisticated Sokoban solver works.
YASS (Yet Another Sokoban Solver), by Brian Damgaard, touts the use of a packing order calculation. I spent many hours trying to figure out what this was, and in the end boiled down the fundamental idea: it is a macro search where, instead of using individual box moves, the actions consist of either pushing a box all the way to a goal tile, or pushing a box as far away from its current position as possible with the hope that that frees up space for other boxes. That’s it.
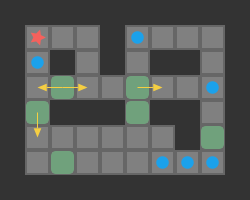
The devil, of course, is in the details. YASS has a lot of additional bells and whistles, such as using deadlock sets and a special phase in which a box comes from a relatively small area of the board. This post merely looks at the core idea.
A Coarser Problem Representation
As mentioned above, most Sokoban solvers reason about pushes. This is already a coarser problem representation than basic Sokoban, where the actions are individual player moves. The coarser representation significantly reduces the size of the search tree. The player can move in four directions, so by collapsing ten moves that lead to a box push we can nicely remove O(4^10) possible states in our search tree.
Generally speaking, reasoning with a coarser problem representation lets us tackle larger problems. The larger, “chunkier” actions let us get more done with less consideration. The trade-off is that we give up fine-tune adjustments. When it comes to player moves vs. box pushes this is often well worth it. For the macro moves in packing order calculations, that is less true. (More on that later).
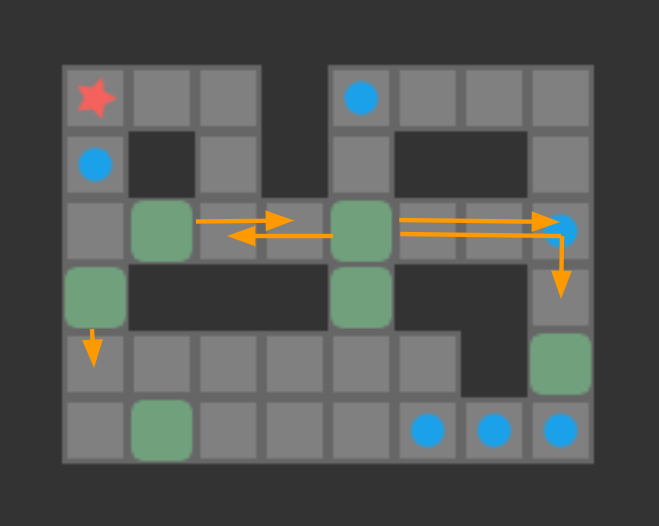
If we solve a problem in a coarser representation, we need to be able to transform it back into the finer representation:
Transforming box pushes back into player moves is easy, as we simply find the shortest path for the player to the appropriate side of the box, and then tack on the additional step to push the box. In this case, we have a well-defined way to find the (locally) optimal sequence of player moves in order to complete the push.
The macro actions taken in the pure version of the packing order calculation I implemented work the same way. We simply calculate the push distance between tiles and find the shortest push path to the destination tile. As such, packing order macro actions are converted to pushes, which in turn can be converted to player moves.
Packing Order Search
Search problems are defined by their states, actions, . Our coarser problem for packing order search is:
States – the same as Sokoban, augmented with an additional state for each box. For each box, we keep track of whether it is:
- unmoved
- temporarily parked
- permanently parked
Actions:
- An unmoved box can either be temporarily parked or pushed all the way to a goal, assuming the destination is reachable only by pushing that box.
- A temporarily parked box can be pushed all the way to a goal, assuming the destination is reachable only by pushing that box. (It cannot be temporarily re-parked.)
YASS computes up to two candidate temporary parking tiles for each box:
- the farthest tile in Manhattan distance from the box’s current position
- the farthest tile in push distance from the box’s current position
Goals – the same as Sokoban. All boxes on goals.
Several things are immediately apparent. First, we can bound the size of our search tree. Every box can be moved at most twice. As such, if we have b boxes, then we can have at most 2^b macro actions. This in turn makes it obvious that not every problem can be solved with this search method. The search method, as is, is incomplete. Many Sokoban problems require moving a single box multiple times before bringing it to a goal. We could counteract that by allowing multiple re-parks, but we quickly grow our search tree if we do so.
The number of actions in a particular state is fairly large. A single box can be pushed to every goal it can reach, and can be parked on up to two possible candidate tiles. Since the number of goals is the same as the number of boxes, this means we have up to (2+b)^b actions in a single state. (Typically far less than that). As such, our tree is potentially quite fanned out. (In comparison, solving for box pushes has at most 4b actions in a single state).
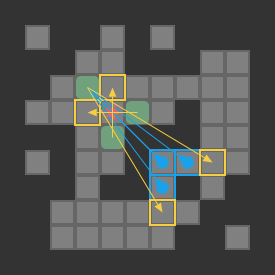
We can apply pretty much any of the basic search algorithms from my previous post to this coarser problem representation. I just went with a basic depth-first search.
Below we can see a solution for a basic 3-box problem, along with its backed-out higher-fidelity versions:
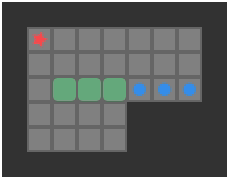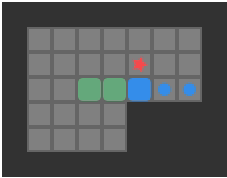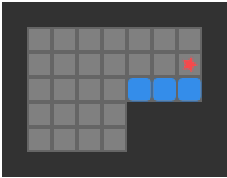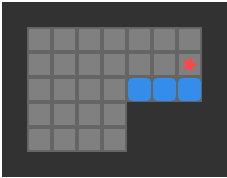
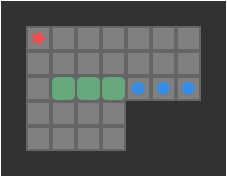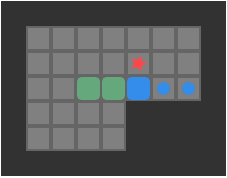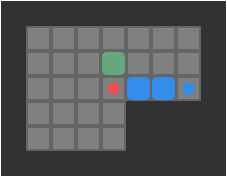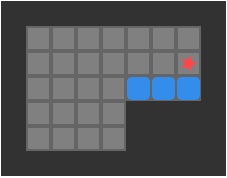
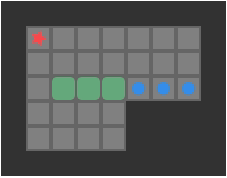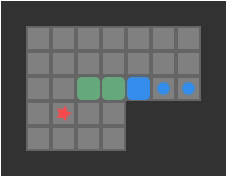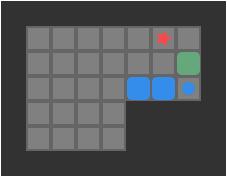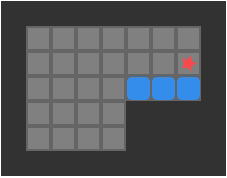
While illustrative and a neat experience, this basic depth-first packing order search is not particularly great at solving Sokoban problems. It does, however, nicely illustrate the idea of translating between problem representations.
Reverse Packing Order Search
The packing order calculation done by YASS performs its search in reverse. That is, rather than starting with the initial board state and trying to push boxes to goals, it starts with all boxes on goals and tries to pull them to their starting states.
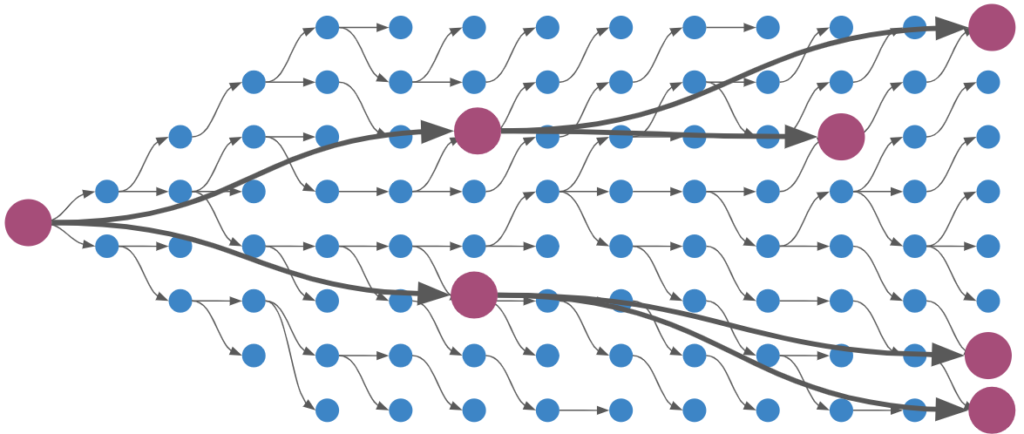
Reverse search and its various forms (ex: bidirectional search), are motivated by the fact that searching in the forward direction alone may not be as easy as the reverse direction. One common example is a continuous-space path finding problem in which the search has to find a way through a directional bottleneck:
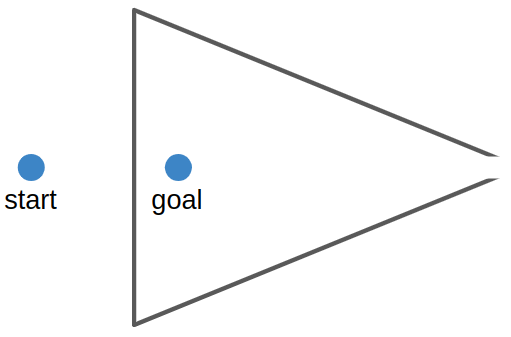
The motivation for a reverse search in Sokoban is similar. However, rather than having to thread the needle through directional bottlenecks, Sokoban search has to avoid deadlock states. Reverse search is motivated by the idea that it is easier to get yourself into a deadlock state by pushing boxes than it is to get yourself into deadlock states by pulling boxes. This technique is presented in this paper by Frank Takes. Note that deadlocks are still possible – they just occur less frequently. That being said, 2×2 deadlocks won’t occur, the box cannot be pulled up against a wall or in a corner, etc.
The starting state in a reverse search is a goal state – all boxes on goals. Note that we do not know where the player should start – they would end up next to one of the boxes. As such, we have to consider all player-reachable regions surrounding the goals. Below we show the initial state for a problem and three possible reverse search start states:




My simple solver simply tries each possible start state until it finds a solution (or fails after exhausting all possibilities).
Reverse packing order search does perform than packing order search. It still suffers from incompleteness, and would need to be fleshed out with more bells and whistles to be useful (deadlock analysis, goal room packing, etc.). That being said, we can solve some problems that are too big for my previous version of A*, such as Sasquatch 49. We solve it in 0.002s.

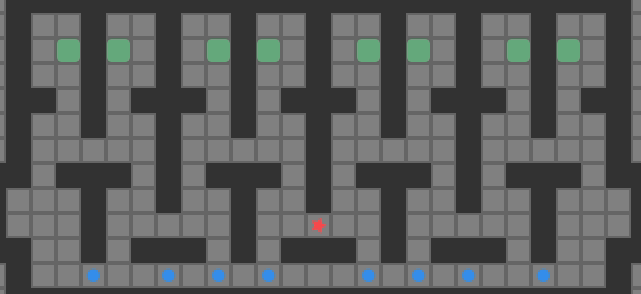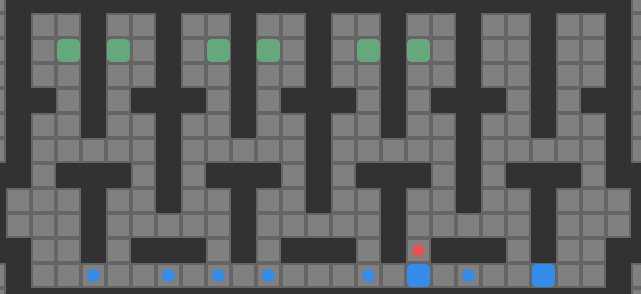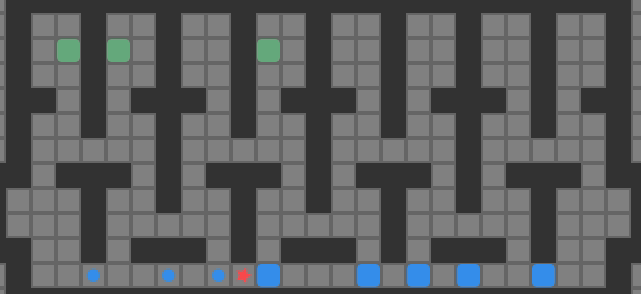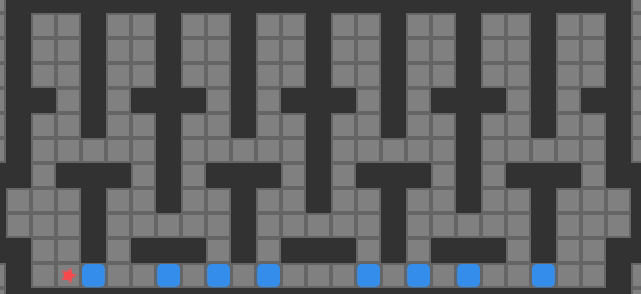
So there you have it, a simple solver that can handle an 8-box problem. Granted, it cannot solve most 8-box problems, but we have blazed a bit of a trail forward.
Conclusion
The main takeaway here is that one of the best ways to scale to larger problems is to reason with a coarser problem representation. We don’t plan every footstep when deciding to walk to the kitchen. Similarly, we reason about overall street routes when planning to drive somewhere, rather than thinking about every lane change (usually). Multi-level planning can be incredibly powerful – we just have to be careful to be able to back out feasible solutions, and not miss important details.