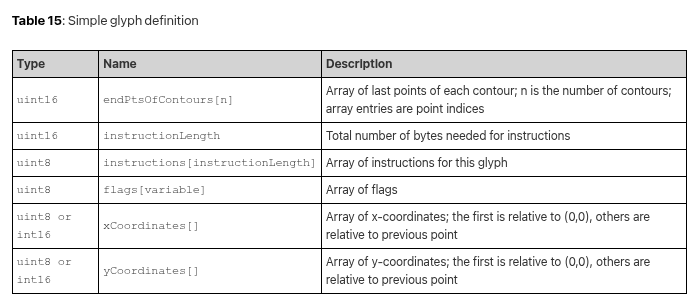
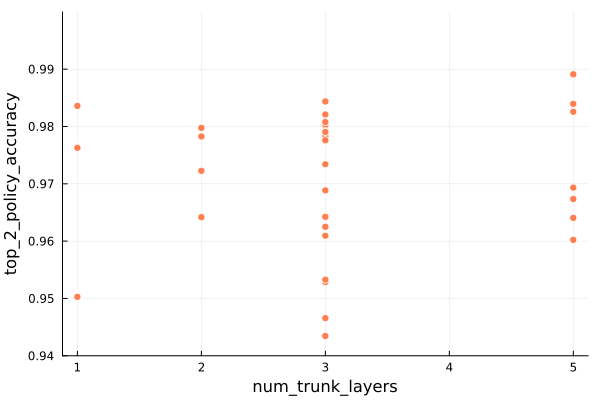
Current title screen using text rendering with the Arial TrueType fonts.
Last month we covered text rendering, which was necessary for getting the scaffolding up that supports the over-arching gameplay loop. We have a title screen, a level select screen, codex screens for seeing information about unlocked heroes and relics, and a level results screen that summarizes what was gained when completing a level. All of these are rudimentary first stabs, but ya got to make it exist first.
A lot happened in the last month, some of which I might cover in future posts. I’m not going to list everything every time, but it is interesting to see just how much stuff goes into making some sort of usable interactive experience when you’re doing a lot from scratch.
- Added basic hero avatars to display when the hero is selected.
- Added a tweak file system for rapidly tuning parameters.
- Expanded the hero struct to include a hero level state to distinguish between in-level heroes and those that have not yet been deployed and those that have exited a level.
- Added new screens.
- Generalized my UI panel work to have fancier button logic that properly detects button presses, accounting for when the player clicks elsewhere but releases over the button, or presses down on the button but releases elsewhere.
- Moved the game interface to simply receive one large memory buffer that the game itself then chops up into whatever smaller allocations and arenas it needs.
- Introduced local mesh assets that can be directly rendered via the triangle shader from the previous post, used for basic quads and things like the selection outline.
- Introduced the grid view. More on that in a bit.
- Added a way to quickly identify which entities are in which cells in the stage, now more necessary due to the grid view.
- Introduced schedules and simulating consequences up front rather than live.
- Added the action selection panel and action sub-selection interfaces for hero deployment, move selection, and turn passing. The focus of this blog post.
- Removed a bunch of earlier code pre-move selection where the active hero would move one tile or perform one action per key press.
The game now looks like this:
Obviously, all art, layout, UI, etc. is an extremely early first cut and likely not the final version. We do, however, see the basic framework for a game.
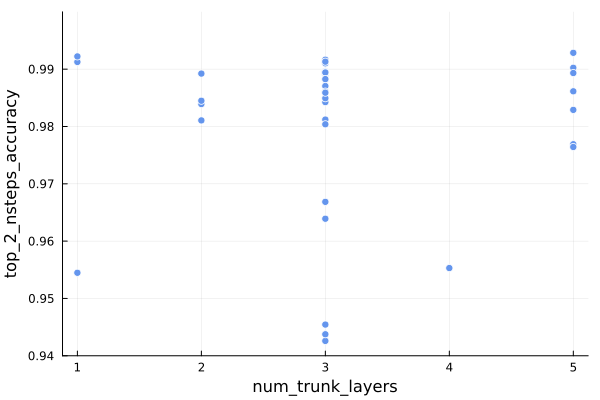
Action Panel
The main thing I want to talk about this week is the fledgling action system, starting with the action panel:
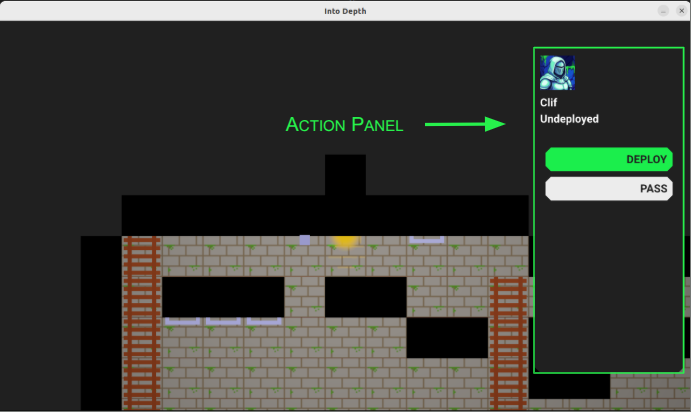
The action panel shows the active hero’s avatar, their name, their level state, and has a series of action buttons.
You’ll notice that the panel has the same color as the background. Eventually, when the field of view includes shadow casting, it should just blend with the shadows. Here is my Google slides mockup of what I’m roughly working toward:
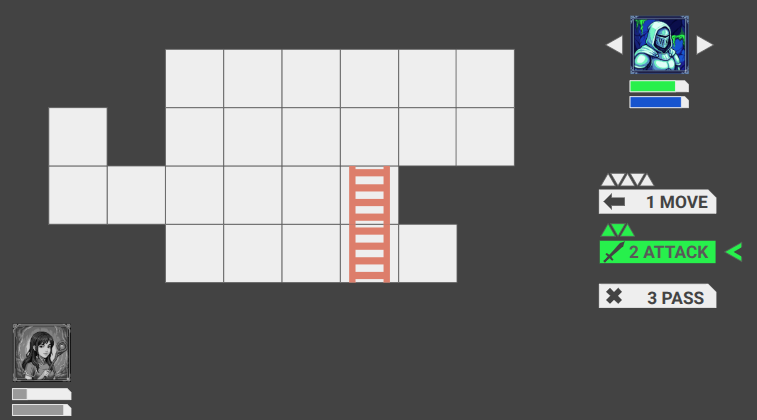
Eventually we’ll see the whole party, along with whatever status bars we need to see, and the actions available to the hero will look fancier. Most notably, I intend to render little equilateral triangles to represent the action points available for various moves. I’m not 100% settled on how that would work, but something like that will happen.
The game loop inside a level tracks which actor is active, and then loops through four states:
- Generate Actions
- Select Action
- Play Schedule
- Done
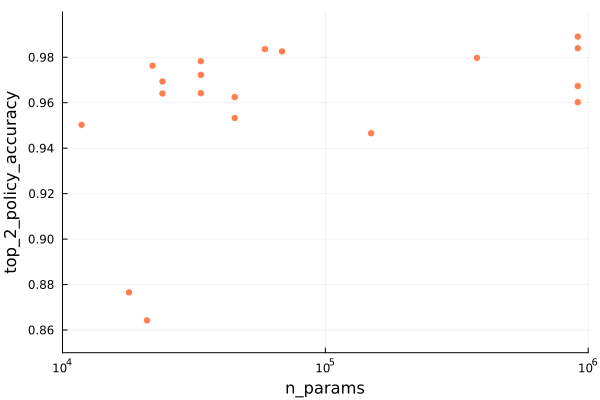
The first state is where the game looks at the current state and generates the actions available to the actor. For heroes, these then show up as options in the action panel. The user can then select an action and get access to its dedicated UI, and use that to determine the details.
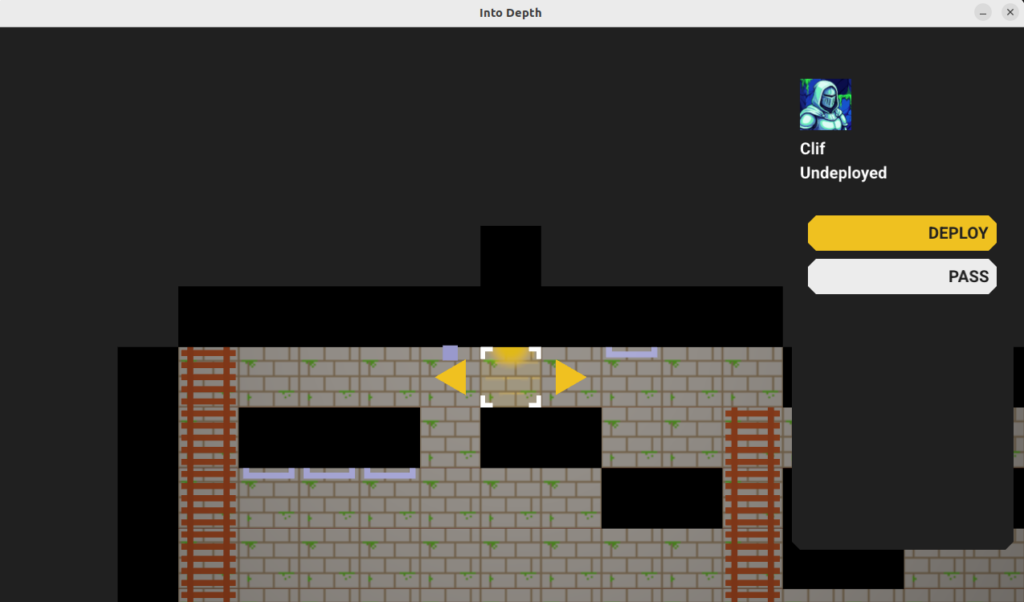
Here we’ve selected the DEPLOY action and we get a user interface for selecting which cell to deploy the hero to.
Once the user commits to an action, the action generates a schedule. This is the sequence of events that represent the outcome of the action. For example, passing the turn simply produces an event that moves the game to the next actor. Selecting a move to a cell produces a more complicated schedule that traverses multiple cells in sequence, and may involve posture changes like changing from standing to climbing.
Most importantly, a schedule contains the complete outcome of the action. Previously, if the actor planned to move, I was having the game check live, as the player moved, for triggered events like ending up over an empty shaft and then moving into a falling state. This fragments the logic and makes it harder to test planning and consequence code, as we don’t really know the consequence of an action until it is tediously simulated out over many iterations.
Instead, the schedule does all necessary consequence simulation during construction, and the game then just needs to play that out until it has completed. Given that we have the schedule, it is also quite easy to undo the entire action without having to figure out some weird reverse simulation.
This doesn’t look terribly complicated to implement, but it is actually the system that flummoxed me the most in my previous project attempt, particularly when it came to changing which actions were available based on the actor’s equipment and in enabling undo. I am much happier with how this latest rendition is set up.
The schedule is, at its core, just a DAG of events stored in a topological order:
struct Schedule {
// Events are in a topological order
u16 n_timeline;
Event* timeline; // allocated on the Active linear allocator
// The net outcome.
u16 n_outcome;
Event* outcomes; // allocated on the Active linear allocator
// The opposite of the net outcome, since events are not inherently reversible.
u16 n_undo;
Event* undos; // allocated on the Active linear allocator
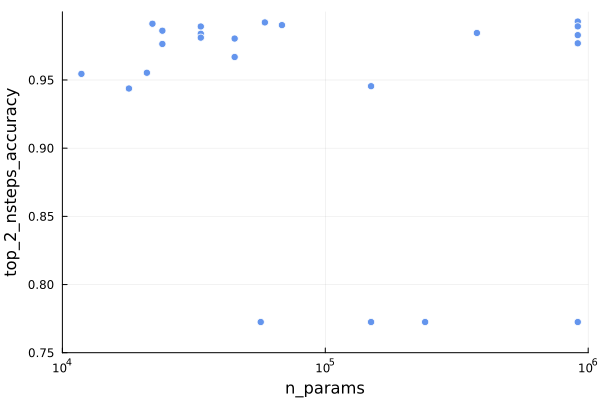
};The schedule contains the full timeline, plus a compressed net outcome that only contains the events necessary to encode the overall delta. For something like a pass action, the timeline and the outcome are the same. For a move, where the actor traverses multiple cells, the timeline contains the sequence of cell traversals but the outcome only contains one cell change – from source to dest.
The schedule also contains the set of events needed to undo the action. This is very similar to the outcome, just reversed. The game events don’t all contain the information necessary to be reversed, so we construct the undo events separately.
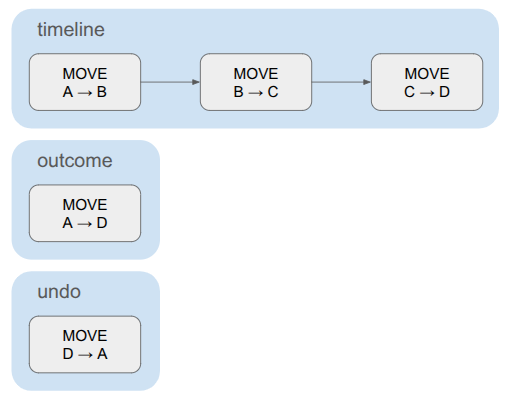
A simple schedule for moving a hero. The timeline contains multiple cell transitions, but the outcome and undo each consist of a single event.
Events are small, composable game state deltas:
struct Event {
u16 index; // The event's index in the schedule. (Events are in a topological order)
u16 beat; // The beat that this event should be executed on. Events sharing a beat happen concurrently.
EventType type;
union {
EventEndTurn end_turn;
EventSetHeroLevelState set_hero_level_state;
EventMove move;
EventSetCellIndex set_cell_index;
EventSetFacingDir set_facing_dir;
EventSetHeroPosture set_hero_posture;
EventAttachTo attach_to;
EventOnBelay on_belay;
EventOffBelay off_belay;
EventHaulRope haul_rope;
EventLowerRope lower_rope;
... etc.
};
};Each event knows its event type and then contains type-specific data. This is a pretty straightforward way to interleave them without annoying object-oriented inheritance code.
Events also contain beats. The game logic is discrete, and in order to have events run concurrently, we store them in the same beat:
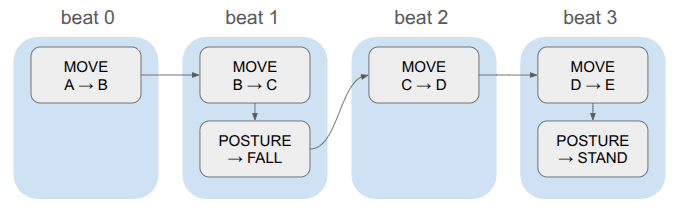
Whenever we advance a beat, we apply all events in that beat and trigger any animations or whatnot and use that to determine how long to wait until we start the next beat. This keeps the event system clean (it doesn’t need to know how long a given animation will take, or even what animation is associated with an event), and gives us one centralized place for triggering animations and sounds.
When the schedule is fully played out, the game enters the done state and checks to see if the level is done. If not, it goes back to action generation.
The state for active levels thus includes the core game state (the stage), which actor’s turn it is, the active schedule (if any), the schedule playback state (event index, time in beat), and data for all of this turn’s actions:
struct ScreenState_Active {
// The active playable area and the entities in it.
Stage stage;
// Stores data for the active actor's turn.
Turn turn;
// Stores the events that are scheduled to run.
Schedule schedule;
// The playback state of the schedule.
PlaybackState playback_state;
// The index of the active actor.
int i_actor = 0;
int i_actor_next;
// Where we allocate the action data.
// This allocator is only reset when actions are regenerated.
LinearAllocator action_allocator;
};Pretty clean when it comes down to it.
The Turn contains the actions generated for the current actor. Each action has a name, which then makes it easy to render the buttons for the actions in the action panel.
Actions
An action is a discrete state change available to an actor, such as passing the turn, moving through the environment, or attacking another actor. The available actions depend on the game state — an actor that is not yet deployed has a deploy action but no move action, and an actor with a bow should get an attack action with a ranged UI whereas an actor with a sword can only select the tiles within melee range.
To handle these things flexibly, actions have methods that can be specialized on a per-action basis. In modern C++, one would probably use objects and inheritance to implement a bunch of action subclasses. I am avoiding classes and , so instead we have a basic struct with some function pointers:
// A function pointer called to run the action UI for the action,
// once the action has been selected in the menu.
typedef void (*FuncRunActionUI)(GameState* game, RenderCommandBuffer* command_buffer, void* data, const AppState& app_state);
// A function pointer for a method that determines whether the action was committed.
typedef bool (*FuncIsActionCommitted)(const void* data);
// A function pointer for a method that builds a schedule from the action.
typedef bool (*FuncBuildSchedule)(GameState* game, void* data);
struct Action {
char name[16]; // null-terminated
// The key to press to perform this action
char shortkey;
// Data associated with the action, specialized per action type
void* data;
// Function pointers
FuncRunActionUI run_action_ui;
FuncIsActionCommitted is_action_committed;
FuncBuildSchedule build_schedule;
};We use the action name when displaying its button in the action panel, and its shortkey is available if the user doesn’t want to have to click the button with the mouse.
Each action also has a void* data member, which can be populated when the action is created and then used in the member functions. We’ll see an example of that shortly.
Generating the available actions is conceptually straightforward; just run a method for every action in the game that checks if that action is available, and if it is, allocates it, constructs it, and adds it to the action list:
void GenerateActions(GameState* game, const Hero& hero) {
Turn& turn = game->screen_state_active.turn;
turn.n_actions = 0;
turn.i_action_selected = -1;
if (MaybeGenerateAction_Deploy(&turn.actions[turn.n_actions], game, hero)) {
turn.n_actions++;
}
if (MaybeGenerateAction_Move(&turn.actions[turn.n_actions], game, hero)) {
turn.n_actions++;
}
if (MaybeGenerateAction_Pass(&turn.actions[turn.n_actions], game, hero)) {
turn.n_actions++;
}
...
}This may seem too simple, but I think it is actually quite an advantage. I had previously been considering having various pieces of equipment be responsible for determining which actions they are associated with, and then having a way to store that metadata on the equipment, save it to disk, etc. Messy! Instead, I can just run all of these methods, every time, and if any require specific equipment, they can check for it and just quickly return false if it isn’t there.
Every action currently requires at least four methods: action generation, running the action-specific UI, a simple method that determines whether the user committed to the action, and a schedule generation. For the simple pass action, this doesn’t even need the void* data member:
// ------------------------------------------------------------------------------------------------
bool MaybeGenerateAction_Pass(Action* action, GameState* game, const Hero& hero) {
strncpy(action->name, "PASS", sizeof(action->name));
action->shortkey = 'p';
action->run_action_ui = RunActionUI_Pass;
action->is_action_committed = IsActionCommitted_Pass;
action->build_schedule = BuildSchedule_Pass;
return true;
}
// ------------------------------------------------------------------------------------------------
void RunActionUI_Pass(GameState* game, RenderCommandBuffer* command_buffer, void* data, const AppState& app_state) {
// Nothing to do here.
}
// ------------------------------------------------------------------------------------------------
bool IsActionCommitted_Pass(const void* data) {
return true;
}
// ------------------------------------------------------------------------------------------------
bool BuildSchedule_Pass(GameState* game, void* data) {
ScreenState_Active& active = game->screen_state_active;
// Build the schedule, which consists just of an end turn action.
Schedule* schedule = &(game->screen_state_active.schedule);
schedule->n_timeline = 1;
schedule->timeline = (Event*)Allocate(&(active.action_allocator), sizeof(Event));
ASSERT(schedule->timeline != nullptr, "BuildSchedule_Pass: Failed to allocate timeline!");
CreateEventEndTurn(schedule->timeline, /*index=*/0, /*beat=*/0);
// The outcome is the same.
schedule->n_outcome = 1;
schedule->outcomes = schedule->timeline;
// The undo action: TODO
return true;
}The deploy action is more involved, and it does allocate a custom data struct:
struct DeployActionData {
// List of legal entry cells for the hero.
u16 n_entries;
CellIndex entries[STAGE_MAX_NUM_ENTRIES];
// The index of the entry we are looking at.
int targeted_entry;
// Whether the entry has been selected.
bool entry_selected;
};
// ------------------------------------------------------------------------------------------------
void InitActionData_Deploy(DeployActionData* data) {
data->n_entries = 0;
data->targeted_entry = 0;
data->entry_selected = false;
}
// ------------------------------------------------------------------------------------------------
bool MaybeGenerateAction_Deploy(Action* action, GameState* game, const Hero& hero) {
if (hero.level_state != HERO_LEVEL_STATE_UNDEPLOYED) {
// Hero does not need to be deployed
return false;
}
ScreenState_Active& active = game->screen_state_active;
const Stage& stage = active.stage;
// Allocate the data for the action
action->data = Allocate(&(active.action_allocator), sizeof(DeployActionData));
DeployActionData* data = (DeployActionData*)action->data;
InitActionData_Deploy(data);
// Run through all stage entries and find the valid places to deploy
for (u16 i_entry = 0; i_entry < stage.n_entries; i_entry++) {
CellIndex cell_index = stage.entries[i_entry];
ASSERT(!IsSolid(stage, cell_index), "Entry cell is solid!");
// Ensure that the cell is not occupied by another hero
if (IsHeroInCell(stage, cell_index)) {
continue;
}
// Add the entry.
data->entries[data->n_entries++] = cell_index;
}
if (data->n_entries == 0) {
// No valid entries
return false;
}
strncpy(action->name, "DEPLOY", sizeof(action->name));
action->shortkey = 'd';
// action.sprite_handle_icon = // TODO
action->run_action_ui = RunActionUI_Deploy;
action->is_action_committed = IsActionCommitted_Deploy;
action->build_schedule = BuildSchedule_Deploy;
return true;
}
// ------------------------------------------------------------------------------------------------
void RunActionUI_Deploy(GameState* game, RenderCommandBuffer* command_buffer, void* data, const AppState& app_state) {
DeployActionData* action_data = (DeployActionData*)data;
const TweakStore* tweak_store = &game->tweak_store;
const f32 kSelectItemFlashMult = TWEAK(tweak_store, "select_item_flash_mult", 2.0f);
const f32 kSelectItemReticuleAmplitude = TWEAK(tweak_store, "select_item_reticule_amplitude", 0.25f);
const f32 kSelectItemFlashAlphaLo = TWEAK(tweak_store, "select_item_flash_alpha_lo", 0.1f);
const f32 kSelectItemFlashAlphaHi = TWEAK(tweak_store, "select_item_flash_alpha_hi", 0.9f);
const f32 kSelectItemArrowOffsetHorz = TWEAK(tweak_store, "select_item_arrow_offset_horz", 1.0f);
const f32 kSelectItemArrowScaleLo = TWEAK(tweak_store, "select_item_arrow_scale_lo", 1.0f);
const f32 kSelectItemArrowScaleHi = TWEAK(tweak_store, "select_item_arrow_scale_hi", 1.0f);
// TODO: This is probably lagged by one frame.
const glm::mat4 clip_to_world = CalcClipToWorld(command_buffer->render_setup.projection, command_buffer->render_setup.view);
const glm::vec2 mouse_world = CalcMouseWorldPos(app_state.pos_mouse, 0.0f, clip_to_world, app_state.window_size);
bool deploy_hero_to_target_cell = false;
// Set the hero's location to one tile over the entry we are looking at.
// This is a hacky way to handle the fact that the hero is not in the level yet
// and that the camera is centered on the hero
ScreenState_Active& active = game->screen_state_active;
Hero* hero = active.stage.pool_hero.GetMutableAtIndex(active.i_actor);
const CellIndex cell_index = action_data->entries[action_data->targeted_entry];
MoveHeroToCell(&active.stage, hero, {cell_index.x, (u16)(cell_index.y + 1)});
hero->offset = {0.0f, 0.0f};
// Render the entrance we are currently looking at.
{
const f32 unitsine = UnitSine(kSelectItemFlashMult * game->t);
RenderCommandLocalMesh& local_mesh = *GetNextLocalMeshRenderCommand(command_buffer);
local_mesh.local_mesh_handle = game->local_mesh_id_quad;
local_mesh.screenspace = false;
local_mesh.model = glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, -1.0f, RENDER_Z_FOREGROUND));
local_mesh.color = kColorGold;
local_mesh.color.a = Lerp(kSelectItemFlashAlphaLo, kSelectItemFlashAlphaHi, unitsine);
{
RenderCommandLocalMesh& reticule = *GetNextLocalMeshRenderCommand(command_buffer);
reticule.local_mesh_handle = game->local_mesh_id_corner_brackets;
reticule.screenspace = false;
reticule.model = glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, -1.0f, RENDER_Z_FOREGROUND + 0.1f));
reticule.model = glm::scale(reticule.model, glm::vec3(unitsine * kSelectItemReticuleAmplitude + 1.0f));
reticule.color = kColorWhite;
}
// Run button logic on the targeted entry.
const Rect panel_ui_area = {
.lo = glm::vec2(- 0.5f, - 1.5f),
.hi = glm::vec2(+ 0.5f, - 0.5f)};
const UiButtonState button_state = UiRunButton(&game->ui, panel_ui_area, mouse_world);
if (button_state != UiButtonState::NORMAL) {
local_mesh.color.x = Lerp(local_mesh.color.x, kColorWhite.x, unitsine);
local_mesh.color.y = Lerp(local_mesh.color.y, kColorWhite.y, unitsine);
local_mesh.color.z = Lerp(local_mesh.color.z, kColorWhite.z, unitsine);
}
if (button_state == UiButtonState::TRIGGERED) {
deploy_hero_to_target_cell = true;
}
}
bool pressed_left = IsNewlyPressed(app_state.keyboard, 'a');
bool pressed_right = IsNewlyPressed(app_state.keyboard, 'd');
// Render two arrow-like triangles that let us switch between options.
{
const f32 unitsine = UnitSine(game->t);
const f32 scale = Lerp(kSelectItemArrowScaleLo, kSelectItemArrowScaleHi, unitsine);
const glm::vec2 halfdims = glm::vec2(0.433f * scale, 0.5f * scale); // NOTE: Rotated
{ // Left triangle
const glm::vec2 pos = glm::vec2(-kSelectItemArrowOffsetHorz, -1.0f);
const Rect panel_ui_area = {
.lo = pos - halfdims,
.hi = pos + halfdims};
const UiButtonState button_state = UiRunButton(&game->ui, panel_ui_area, mouse_world);
RenderCommandLocalMesh& local_mesh = *GetNextLocalMeshRenderCommand(command_buffer);
local_mesh.local_mesh_handle = game->local_mesh_id_triangle;
local_mesh.screenspace = false;
local_mesh.model =
glm::scale(
glm::rotate(
glm::translate(glm::mat4(1.0f), glm::vec3(pos.x, pos.y, RENDER_Z_FOREGROUND)),
glm::radians(90.0f),
glm::vec3(0.0f, 0.0f, 1.0f)
),
glm::vec3(scale, scale, 1.0f)
);
local_mesh.color = kColorGold;
if (button_state != UiButtonState::NORMAL) {
local_mesh.color = glm::mix(local_mesh.color, kColorWhite, unitsine);
}
// Check for pressing the button.
if (button_state == UiButtonState::TRIGGERED) {
pressed_left = true;
}
}
{ // Right triangle
const glm::vec2 pos = glm::vec2(kSelectItemArrowOffsetHorz, -1.0f);
const Rect panel_ui_area = {
.lo = pos - halfdims,
.hi = pos + halfdims};
const UiButtonState button_state = UiRunButton(&game->ui, panel_ui_area, mouse_world);
RenderCommandLocalMesh& local_mesh = *GetNextLocalMeshRenderCommand(command_buffer);
local_mesh.local_mesh_handle = game->local_mesh_id_triangle;
local_mesh.screenspace = false;
local_mesh.model =
glm::scale(
glm::rotate(
glm::translate(glm::mat4(1.0f), glm::vec3(pos.x, pos.y, RENDER_Z_FOREGROUND)),
glm::radians(-90.0f),
glm::vec3(0.0f, 0.0f, 1.0f)
),
glm::vec3(scale, scale, 1.0f)
);
local_mesh.color = kColorGold;
if (button_state != UiButtonState::NORMAL) {
local_mesh.color = glm::mix(local_mesh.color, kColorWhite, unitsine);
}
// Check for pressing the button.
if (button_state == UiButtonState::TRIGGERED) {
pressed_right = true;
}
}
}
// Process the presses, which can come from keys or clicking the arrows.
if (pressed_left) {
CircularDecrement(action_data->targeted_entry, (int)action_data->n_entries);
} else if (pressed_right) {
CircularIncrement(action_data->targeted_entry, (int)action_data->n_entries);
}
if (deploy_hero_to_target_cell) {
action_data->entry_selected = true;
}
}
// ------------------------------------------------------------------------------------------------
bool IsActionCommitted_Deploy(const void* data) {
const DeployActionData* action_data = (DeployActionData*)data;
return action_data->entry_selected;
}
// ------------------------------------------------------------------------------------------------
bool BuildSchedule_Deploy(GameState* game, void* data) {
ScreenState_Active& active = game->screen_state_active;
const Hero* hero = active.stage.pool_hero.GetAtIndex(active.i_actor);
const CellIndex src = hero->cell_index;
const CellIndex dst = {src.x, (u16)(src.y - 1)};
// Build the schedule, which changes the hero's level state and moves them to the entry (1 cell down).
Schedule* schedule = &(game->screen_state_active.schedule);
{
schedule->n_timeline = 2;
schedule->timeline = (Event*)Allocate(&(active.action_allocator), schedule->n_timeline * sizeof(Event));
ASSERT(schedule->timeline != nullptr, "BuildSchedule_Deploy: Failed to allocate timeline!");
CreateEventSetHeroLevelState(schedule->timeline, /*index=*/0, /*beat=*/0, hero->id, HERO_LEVEL_STATE_IN_LEVEL);
CreateEventMove(schedule->timeline + 1, /*index=*/1, /*beat=*/0, hero->id, Direction::DOWN, src, dst);
}
// The outcome is the same.
schedule->n_outcome = 1;
schedule->outcomes = schedule->timeline;
// Undo: TODO
return true;
}Move Actions
The move action is significantly more complicated than the deploy or pass actions.
The move action highlights all valid target cells, allowing the player to select one to move to. Once selected, the shortest path to that cell is taken by the hero, and all consequences are simulated (e.g. falling, triggering a trap) and built into a schedule.
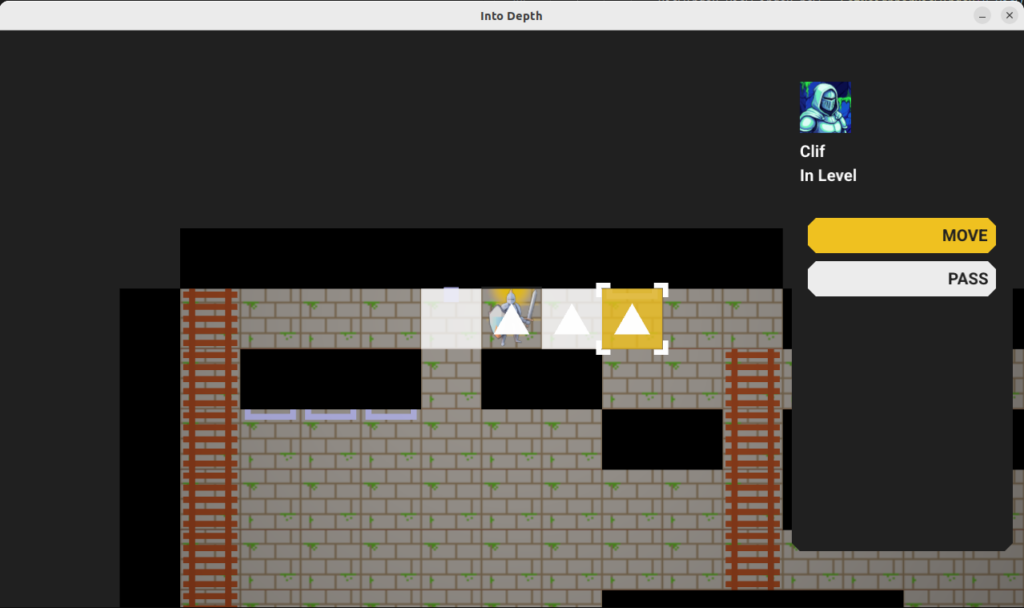
The move action UI, which here has three valid target cells (since falling ends the search). The tile under the mouse cursor is highlighted in yellow, has square angle brackets, and the shortest path is shown as a trail of equilateral triangles.
In order to support these features, the move action logic needs to know what the reachable cells are and what the shortest paths to them are. This is achieved by running Dijkstra’s algorithm from the actor’s initial state. The state space is not merely cell positions, but also includes the actor’s facing direction and their posture (standing, on ladder, etc.).
There is one additional point of complication, and that is that we want this game to only reason about cells that are visible from the hero’s current vantage point, and we eventually want to support non-Euclidean connections like portals:
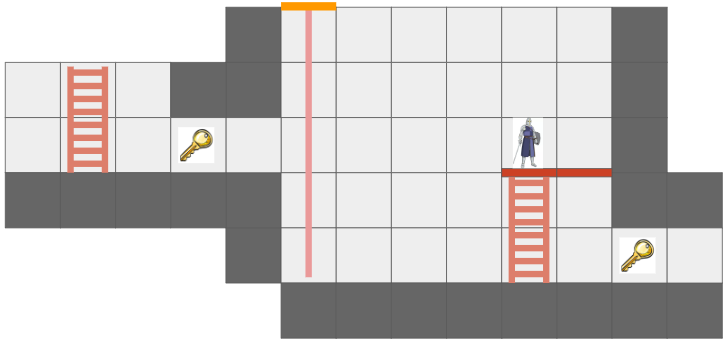
In this mockup, the key is visible twice because the hallway has a portal loop-back connection.
In order to achieve this, we introduce a new representation of the level geometry visible to an actor, the GridView:
struct GridView {
// The grid tile the view is centered on
CellIndex center;
CellIndex cell_indices[GRID_VIEW_MAX_X][GRID_VIEW_MAX_Y];
u8 flags[GRID_VIEW_MAX_X][GRID_VIEW_MAX_Y];
};This view has a finite size, much smaller than the overall level grid, that is big enough to fit the screen. The view is always centered on an actor, and the cells in the view are then indices into the cells in the underlying level grid. If a level grid cell is connected by a non-Euclidean portal to another cell, the view can just index into the correct cells on either side of the portal. Constructing the grid view is a straightforward breadth-first search from the center tile.
Note: I am actually temporarily making this simpler than it really is. To do this properly, we’ll need a fancier data structure that is not a grid but can handle sectors, because one view cell may actually contain view sectors of multiple level cells:
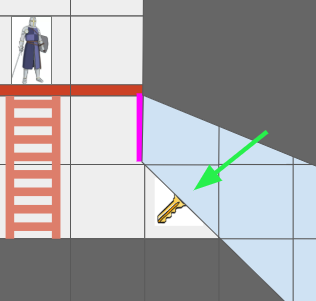
This view cell is visible twice, once with a cell containing a key, with this portal (magenta) set up.
We thus run Dijkstra’s algorithm in this grid view, starting from the center cell where the actor is. The same cell may be visible multiple times in the grid view, and we will correctly be able to route to that cell via multiple paths.
The search assigns a cost for each state change, and only searches up to a maximum cost. Very soon, actors will have action points to spend per turn, and it won’t be possible to move further than are affordable given the action points currently available.
The move action custom data struct is:
struct MoveActionData {
// We can only ever move to a visible tile, so for now, we can
// just allocate a grid's worth of potential targets.
// The cheapest cost to reach each move state.
u16 costs[GRID_VIEW_MAX_X][GRID_VIEW_MAX_Y][/*num directions=*/2][kNumHeroPostures];
// The parent state on the shortest path that arrives at the given state.
// I.E., if [1][2][LEFT][STANDING] contains {2,2,LEFT,STANDING}, then we took a step over.
// The root state points to itself.
MoveState parents[GRID_VIEW_MAX_X][GRID_VIEW_MAX_Y][/*num directions=*/2][kNumHeroPostures];
// Used to track whether a view cell has been visited.
u32 visit_frame;
u32 visits[GRID_VIEW_MAX_X][GRID_VIEW_MAX_Y];
ViewIndex view_index_target; // Target view cell index for the move.
bool entry_selected;
};Having completed the search, we are able to render all reachable tiles, render a reticle over the cell the user’s mouse is over, and if the cell is reachable, we can backtrack over the cell’s parents to render the cells traversed to get there. (Since states include more than just cell changes, and we don’t want to render multiple times to the same cell, we also store a u32 visit frame that we can use to mark cells we have rendered to in order to avoid rendering to the same cell multiple times.)
Finally, when the user clicks on a cell to commit the action, we compute the schedule by:
- Extracting the shortest path by traversing back to the source node.
- Writing the shortest path out one state change at a time.
- Simulating consequences (like falling) after every step, and if any consequences do take place, ending the planned schedule there and appending all consequence events.
This process makes a copy of the current state and applies all changes there. Making a copy, while taking memory, has the advantage of not polluting the actual game state and giving us a second Stage to compare the current Stage to in order to get the overall schedule delta.
Conclusion
With the action system in place, the foundation is laid for actual gameplay. Next time, we’ll look at introducing some core entities back in (ropes, buckets, relics) and managing the overall gameplay cycle.