In the previous two posts, we used various control strategies to solve the classic cart-pole problem. In the first, we used a classic LQR controller to stabilize the cart pole in the vicinity of its equilibrium point. In the second, we built a system that could reach stability from anywhere, by forming a hierarchical problem using LQR controllers around various reference states and a top-level search strategy to find the right sequence of controls to reach stability.
All of this was well and good, but what if we change our problem even more drastically?
So far, everything we have worked with has had intimate knowledge of the underlying dynamics. The LQR approach only works because we know the equations of motion, and can take the necessary derivatives to form a linear system. What if we didn’t have those equations of motion? In many real-world cases, we simply don’t. Now we’re going to pretended we don’t know the equations of motion, and will learn a good controller anyways.
From Controls to Reinforcement Learning
We are going to take a journey, leaving the land of controls behind, and head to the realm of reinforcement learning. This land is at first glance completely foreign, but once you get your bearings you begin to realize their strange customs are really just alternate manifestations of things we’re already used to.
Previously, in the land of controls, we derived controllers that produced control inputs to drive the system’s state to equilibrium while minimizing cost. The people of the realm of reinforcement learning do the same thing, except they find policies \(\pi(s)\) that produce actions to drive the system’s state to equilibrium while maximizing reward.
Now, unlike in the land of controls, the people of the realm of reinforcement learning are very used to working on systems where they do not know the equations of motion. They know that a transition function \(T(s’\mid s,a)\) and a reward function \(R(s,a)\) exist, but do not necessarily know what it is. Instead, they allow their agent to interact with its environment, and thereby gain information about these from the state transitions and rewards observed.
In this post I am going to use an actor-critic method. These are covered in chapter 13 of Alg4DM. The “actor” part refers to the fact that we learn a policy that our agent then follows. The “critic” part refers to the fact that we also learn a value function that critiques the agent’s policy. Both are trained in parallel, the critic becoming better at maximizing the critic’s reward, and the critic getting better at reflecting the true value of the actor’s behavior.
Problem Definition
We always start by defining the actual problem we are solving. This is super important. The problem that we solve is always a model of the ground truth. As George Box famously said, “All models are wrong, some models are useful.” The real world doesn’t care that modeling actuator saturation is harder – it will simply do what it always does.
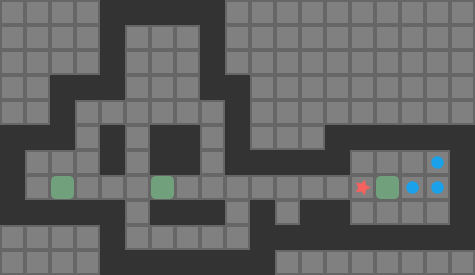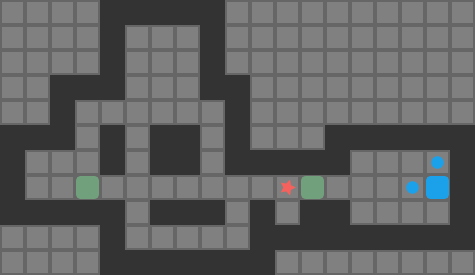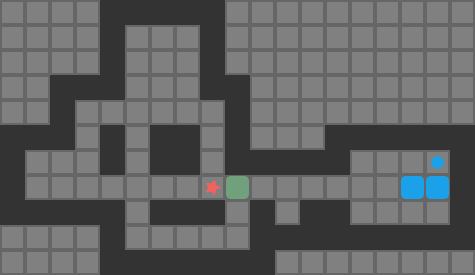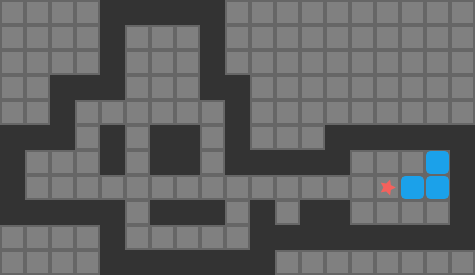
To shake things up a tad, we are going to use cart pole with discrete actions, as it was originally presented. Note that in the land of controls we worked with continuous actions. (We could totally do that here – its just nice to do something different).
Now, the real robot likely can exert continuous forces. We are making a modeling choice, and have to live with the consequences. A series of discrete force outputs will naturally be more jerky / stuttery than a nice smooth output. Maybe we’ll want to tidy that up later, perhaps with a low-pass filter. For now, we’ll go with this.
As such, our problem definition is:
- State Space \(\mathcal{S}\): The same classic cart-pole states consisting of the lateral position \(x\), the lateral velocity \(v\), the pole angle \(\theta\), and the pole’s angular rate \(\omega\).
- Action Space \(\mathcal{A}\): We assume the cart has a maximum actuation force of \(F\). The available actions at each time step (same time step of 50Hz as before) are \(F\), \(0\), and \(-F\). As such, we have three discrete actions.
- Transition Function \(T(s’\mid s, a)\): We use the deterministic cart-pole transition function under the hood, with the same transition dynamics that we have already been using.
- Reward Function \(R(s,a)\): The original paper just gives a reward of 1 any time the cart is in-bounds in \(x\) and \(\theta\). We are instead going to use the reward function formulation that penalizes deviations from stability:
\[R(s,a) = \frac{1}{100}r_x + r_\theta = \frac{1}{100}(\Delta x_\text{max}^2 – x^2) + (1 + \cos(\theta))\]
We continue to give zero reward if we are out of bounds in \(x\), but not in \(\theta\).
Note that our learning system does not know the details of the transition and reward function. Note also that our reward function is non-negative, which isn’t necessary, but can make things a bit more intuitive.
Vanilla Actor Critic
The core ideas of actor-critic are pretty straightforward. We are simultaneously learning a policy and a value function.
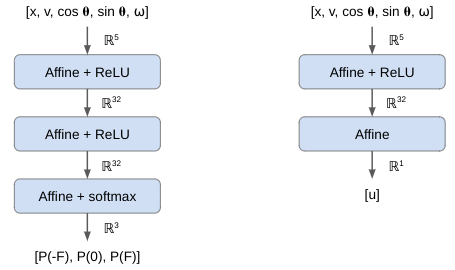
Our policy, (which is stochastic to make the math easier), is a function that produces a categorical distribution over our three actions. We’re going to use a simply deep neural net for this, one with three fully connected layers:
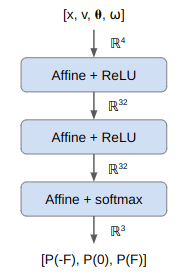
Notice the softmax activation function on the final layer, which ensures that our output is a valid probability distribution.
There are multiple actor-critic approaches with different value functions. In this case I’ll learn a state-value function \(U(s)\), which predicts the expected reward from the given state (the discounted sum of all future rewards). I’m also going to use a simple neural network for this:
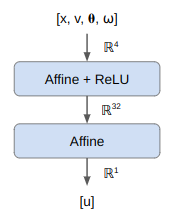
The final layer has no activation function, so the out put can be any real number.
These can both readily be defined using Flux.jl:
get_stochastic_policy(n_hidden::Int=32) = Chain(Dense(4 => n_hidden,relu), Dense(n_hidden => n_hidden,relu), Dense(n_hidden => 3), softmax) get_value_function(n_hidden::Int=32) = Chain(Dense(4 => n_hidden,relu), Dense(n_hidden => 1))
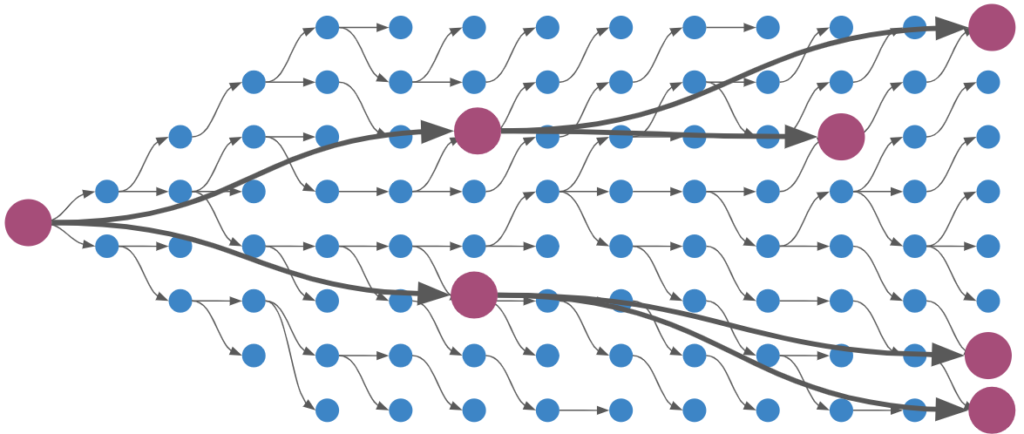
In every iteration we run a bunch of rollouts and:
- compute a policy gradient to get it to maximize the value functions
- compute a value gradient to get our value function to reflect the true expected value
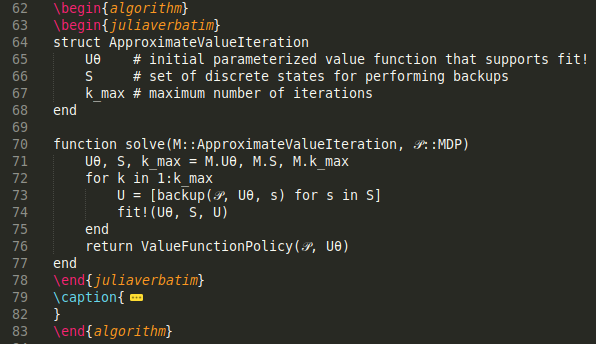
Alg4DM presents this in one nicely compact pseudocode block:

This formulation uses the likelihood ration approach to computing the policy gradient, which for a stochastic policy is:
\[\nabla U(\theta) = \underset{\tau}{\mathbb{E}}\left[\sum_{k=1}^d \gamma^{k-1} \nabla_\theta \log \pi_\theta\left(a^{(k)}\mid s^{(k)}\right) A_\theta\left(s^{(k)},a^{(k)}\right)\right]\]
where we estimate the advantage using our critic value function:
\[A_\theta(s,a) = \underset{r, s’}{\mathbb{E}}\left[ r + \gamma U_\phi(s’) – U_\phi(s)\right]\]
For the critic, we simply minimize the difference between the predicted expected value \(U_\phi(s)\) and the expected value obtained by running the current policy \(U^{\pi_\theta}(s)\):
\[\ell(\phi) = \frac{1}{2}\underset{s}{\mathbb{E}}\left[\left(U_\phi(s) – U^{\pi_\theta}(s)\right)^2\right]\]
The critic gradient is thus:
\[\nabla \ell(\phi) = \underset{s}{\mathbb{E}}\left[ \sum_{k=1}^d \left( U_\phi(s^{(k)}) – r_\text{to-go}^{(k)} \right) \nabla_\phi U_\phi(s^{(k)}) \right]\]
While the math may look a bit tricky, the code block above shows how straightforward it is to implement. You just simulate a bunch of rollouts (\(\tau\)), and then calculate the gradients.
The code I wrote is functionally identical to the code in the textbook, but is laid out a bit differently to help with legibility (and later expansion). Notice that I compute a few extra things so we can plot them later:
function run_epoch( M::ActorCritic, π::Chain, # policy π(s) U::Chain, # value function U(s) mem::ActorCriticMemory, ) t_start = time() 𝒫, d_max, m = M.𝒫, M.d, M.m data = ActorCriticData() params_π, params_U = Flux.params(π), Flux.params(U) ∇π, ∇U, vs, Us = mem.∇π, mem.∇U, mem.vs, mem.Us states, actions rewards = mem.states, mem.actions, mem.rewards a_selected = [0.0,0.0,0.0] # Zero out the gradients for grad in ∇π fill!(grad, 0.0) end for grad in ∇U fill!(grad, 0.0) end # Run m rollouts and accumulate the gradients. for i in 1:m # Run a rollout, storing the states, actions, and rewards. # Keep track of max depth reached. max_depth_reached = rollout(M, π, U, mem) fit!(data.max_depth_reached, max_depth_reached) # Compute the actor and critic gradients r_togo = 0.0 for d in max_depth_reached:-1:1 v = vs[d] s = states[d] a = actions[d] r = rewards[d] s′ = states[d+1] a_selected[1] = 0.0 a_selected[2] = 0.0 a_selected[3] = 0.0 a_selected[a] = 1.0 r_togo = r + γ*r_togo A = r_togo - Us[d] fit!(data.advantage, A) ∇logπ = gradient(() -> A*γ^(d-1)*log(π(v) ⋅ a_selected), params_π) ∇U_huber = gradient(() -> Flux.Losses.huber_loss(U(v), r_togo), params_U) for (i_param,param) in enumerate(params_π) ∇π[i_param] -= ∇logπ[param] end for (i_param,param) in enumerate(params_U) ∇U[i_param] += ∇U_huber[param] end end end # Divide to get the mean for grad in ∇π grad ./= m end for grad in ∇U grad ./= m end data.∇_norm_π = sqrt(sum(sum(v^2 for v in grad) for grad in ∇π)) data.∇_norm_U = sqrt(sum(sum(v^2 for v in grad) for grad in ∇U)) data.w_norm_π = sqrt(sum(sum(w^2 for w in param) for param in params_π)) data.w_norm_U = sqrt(sum(sum(w^2 for w in param) for param in params_U)) data.t_elapsed = time() - t_start return (∇π, ∇U, data) end
Theoretically, that is all you need to get things to work. Each iteration you run a bunch of rollouts, accumulate gradients, and then use these gradients to update both the policy and the value function parameterizations. You keep iterating until the parameterizations converge.
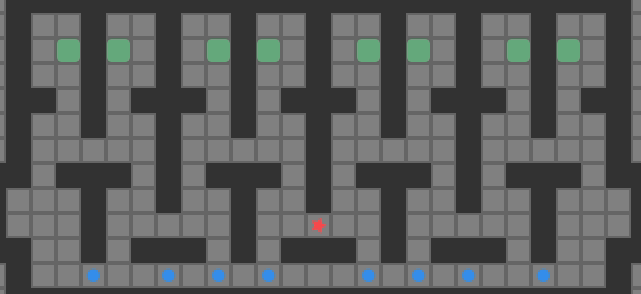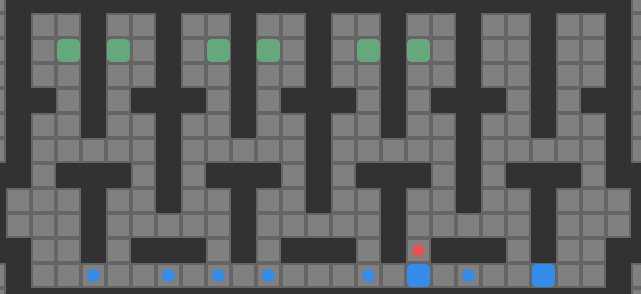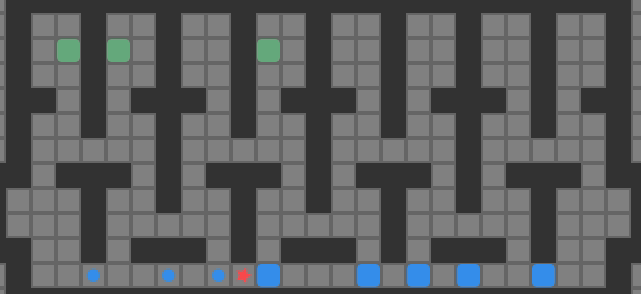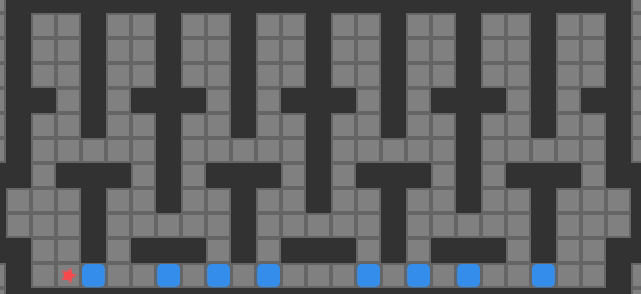
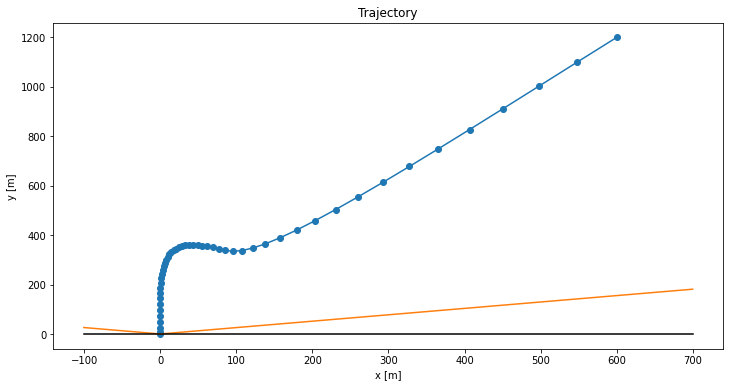
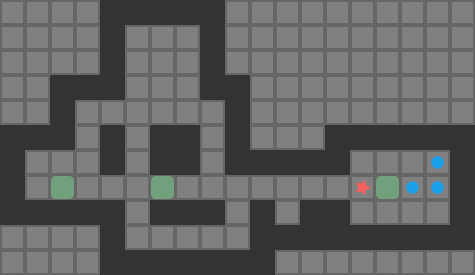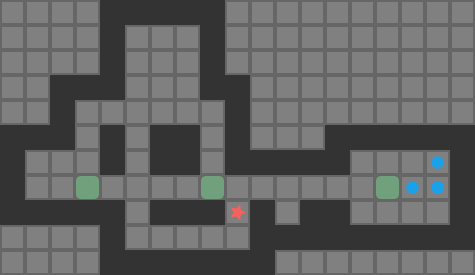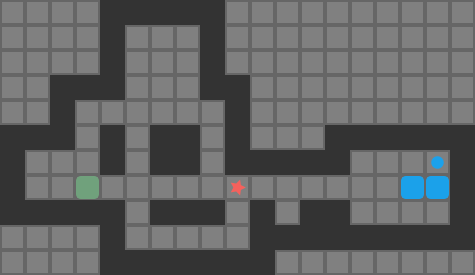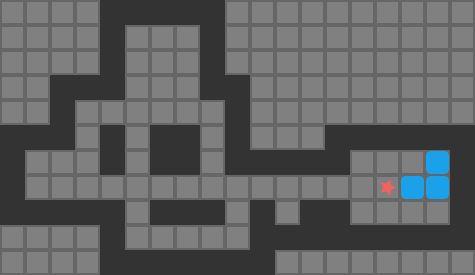
With such an implementation, we get the striking result of….

As we can see, the policy isn’t doing too well. What did we do wrong?
Theoretically, nothing wrong, but practically, we’re missing some bells and whistles that make a massive difference. These sorts of best practices are incredibly important in reinforcement learning (and generally in deep learning).
Decomposing our Angles
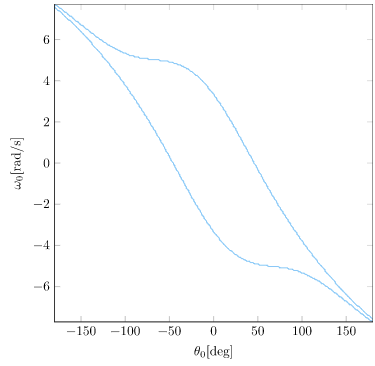
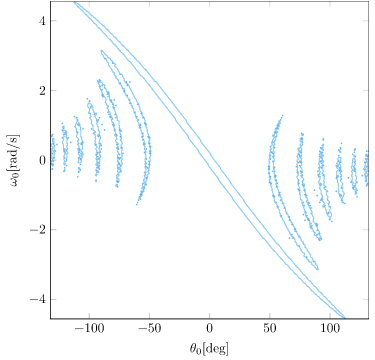
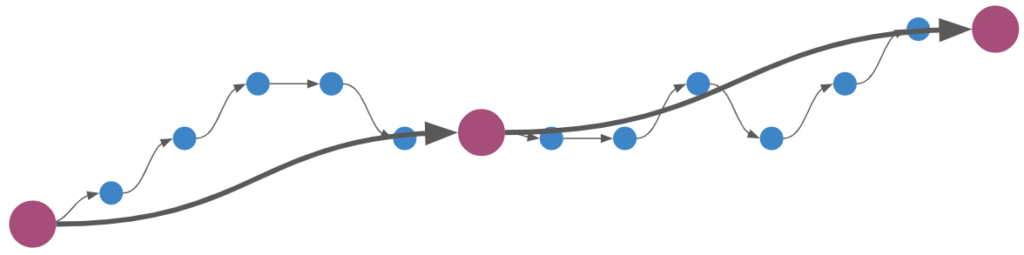
The first change we are going to make is to the inputs to our deep neural net. The current inputs use the raw angle, \(\theta\). This may work well in the basic cart-pole problem where our angle is bounded within a small range, but in a more general cart-pole setting where the pole can rotate multiple times, we end up with weird angular effects that are difficult for a neural network to learn how to handle:
In order to better handle the angle, we are going to instead input \(\cos(\theta)\) and \(\sin(\theta)\):
Wrangling the Loss Functions
One of the biggest issues we have is with the reward function. The expected value at a given state can be quite large. A single state can \(R(s,a)\) produce values as large as 4.8^2/100 + 2 = 2.23, but these then get accumulated over 2000 time steps with a discount factor of \(\gamma = 0.995\), resulting in values as large as \(U(s) = \sum_{k=1}^2000 2.23 \gamma^{k-1} \approx 446\). Now, 446 isn’t massive, but it is still somewhat large. Pretty much everything deep-learning likes to work close to zero.
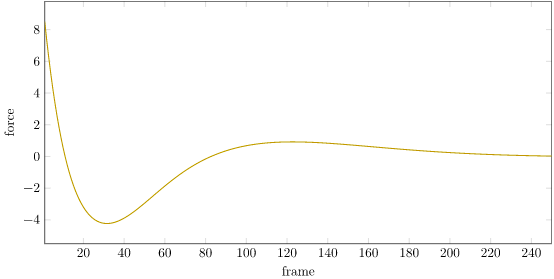
We can plot our gradient norm during training to see how this large reward can cause an issue. The magnitude of the value function gradient is massive! This leads to large instabilities, particularly late in training:
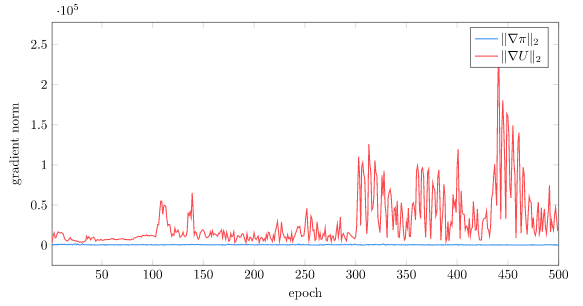
The first thing we will do is dampen out the loss signal for large deviations in reward. Right now, if we predict, say, \(U(s) = 50\) but the real reward is \(U(s) = 400\), we’d end up with a squared loss value of \(350^2 = 122500\). That is somewhat unwieldy.
We want to use a squared loss, for its simplicity and curvature, but only if we are pretty close to the correct value. If we are far off the mark, we’d rather use something gentler.
So we’ll turn to the Huber loss, which uses the squared loss for nearly accurate values and a linear loss for sufficiently inaccurate values:
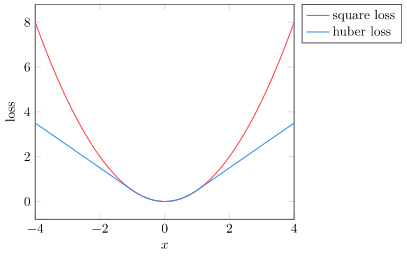
This helps alleviate the large reward problem, but we can do better. The next thing we will do is normalize our expected values. This step adjusts the expected values to have mean zero and a unit standard deviation (i.e., follow a normal distribution):
\[\bar{u} = (u – \mu) / \sigma\]
Right now, our average advantage starts off very large (~150), with a large standard deviation (~50), and over time settles to around mean 0 and stdev 30:
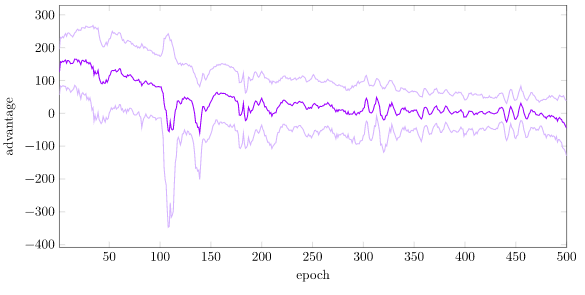
To normalize, we need to keep a running estimate of the value function mean \(\mu\) and standard deviation \(\sigma\). OnlineStats.jl makes this easy. One important thing to note, however, is that we compute the reward-to-go for multiple depths, and the estimated values are going to be different depending on the depth. A reward-to-go from \(k=1\) with a max depth of 2000 is going to be different than a reward-to-go from \(k=1999\). As such, we actually maintain separate mean and standard deviation estimates for each depth.
The last thing we do is clamping, both to the standardized reward-to-go:
r_togo = r + γ*r_togo r_togo_standardized = (r_togo - r_togo_μs[d]) / (r_togo_σs[d] + 1e-3) r_togo_standardized = clamp(r_togo_standardized, -max_standardized_r_togo, max_standardized_r_togo) fit!(r_togo_est[d], r_togo)
and to the gradient:
for grad in ∇π grad ./= m clamp!(grad, -max_gradient, max_gradient) end for grad in ∇U grad ./= m clamp!(grad, -max_gradient, max_gradient) end
Together, these changes allow the value function to predict values with zero-mean and unit variance, which is a lot easier to learn than widely-ranging large values. This is especially important here because the true value function values depend on the policy, which is changing. A normalized reward will consistently be positive for “good” states and negative for “bad” states, whereas a non-normalized will be some large value for “good” states and some not as large value for “bad” states. Normalization thus stabilizes learning.
Regularization
The final change to include is regularization. I am not certain that this makes a huge difference here, but it often does when working with deep learning projects.
Directly minimizing the critic loss and maximizing the expected policy reward can often be achieved with multiple parameterizations. These parameterizations may be on different scales. As we’ve seen before, we don’t like working with large (in an absolute sense) numeric values. Regularization adds a small penalty for large neural network weights, thereby breaking ties and causing the process to settle on a smaller parameterization.
The math is simple if we try to minimize the squared size our parameters:
\[\ell_\text{regularization}(\theta) = \frac{1}{2} \theta^\top \theta\]
Here, the gradient is super simple:
\[\nabla \ell_\text{regularization}(\theta) = \theta\]
We can thus simply add in our parameter values, scaled by a regularization weight:
for (param, grad) in zip(params_π, ∇π) grad += M.w_reg_π * param # regularization term Flux.update!(opt_π, param, grad) end for (param, grad) in zip(params_U, ∇U) grad += M.w_reg_U * param Flux.update!(opt_U, param, grad) end
Putting it all Together
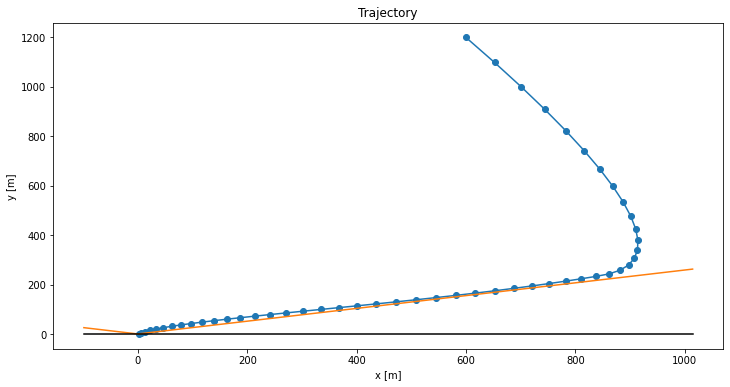
With all of these changes in place, learning is much better. We are able to get Little Tippy the robot to stabilize:

The performance isn’t perfect, because we are, after all, working without explicit knowledge of the system dynamics, and are outputting discrete forces. Nevertheless, this approach was able to figure it out.
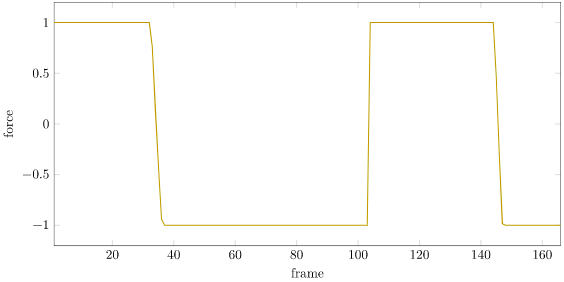
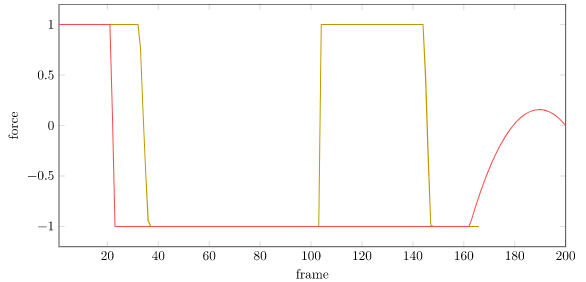
The policy was trained for 500 epochs, each with 128 rollouts to a maximum depth of 1000. A rollout terminates if the cart-pole gets further than 4.8m from the origin. The policy pretty quickly figures out how to stay within bounds: (plus or minus one stdev are also shown):
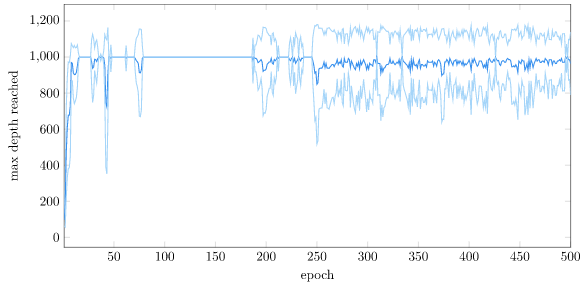
For contrast, here is the same plot with the vanilla setup:
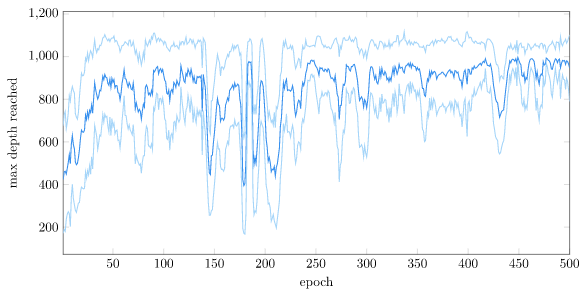
The actual performance is better measured by the mean reward-to-go (i.e., expected value) that the system maintains over time. We can see that we have more-or-less converged:
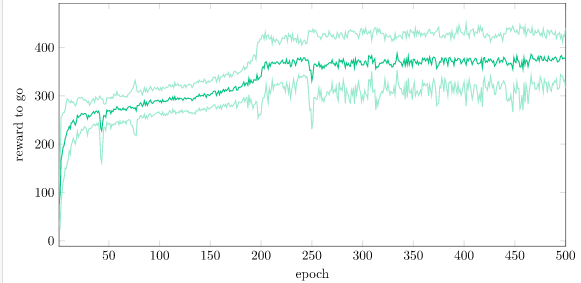
With regularization, our advantage is nicely kept roughly standardized:
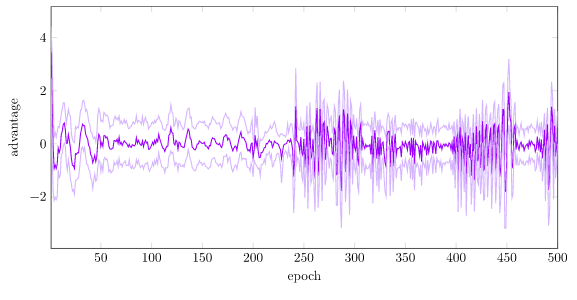
Conclusion
Actor-critic methods are nice for many more general problems, because we often do not know real-world dynamics. Neural networks can be very good function approximations, adapting to the problem at hand (whether that be Go, or an aircraft controller). That being said, actor-critic methods alone are not a panacea, and still require special knowledge and insight. In this post alone, we covered the following decision points that we as a designer made:
- Whether to use discrete actions
- The cart-pole reward function
- Which policy gradient method to use
- Which critic loss function to minimize
- Maximum rollout depth
- Number of rollouts per epoch
- Number of epochs / training termination condition
- Policy neural network architecture
- Critic neural network architecture
- Neural network weight initialization method
- Whether to use gradient clamping
- Using sine and cosine rather than raw angles
- Standardizing the expected value (reward-to-go)
- Which optimizer to use (I used Adam).
Being a good engineer often requires being aware of so much more than the vanilla concepts. It is especially important to understand when one is making a decision, and what impact that design has.
Thank you for reading!
The code for this post is available here. A notebook is here.