With TOOM , I found myself wanting to try something new. So, I started a new vscode workspace and embarked on a new side project – a 2D side scroller.
My overarching goal, once again, is to explore and take it as far as I find it interesting. That being said, I want to overcome the challenge of building a stable game with general 2D physics. By that I mean, “vectorial” physics of the sort used by Braid, with arbitrary 2D level geometry:

Braid level game view and level editor view (image from Higher-Order Fun)
One reason for this goal is that I’ve tried to noodle it out before, but was surprised to find a significant lack of resources. In fact, I had to laugh out loud when I read this excellent heavily cited blog post about 2D platformers. It covers tile-based and rastered platforms in great detail, only to leave vectorial platformers with a vague “you do it yourself” and a warning not to use a physics engine. Well, challenge accepted! Let’s get into it!
There are a few other things I want to learn from this adventure. I plan to eventually use 3D GPU-accelerated graphics. Its worth knowing how that works, and the work on TOOM convinced me that drawing with the CPU is super slow. The aesthetic I have in mind is pretty low-poly, so while I’d normally go with pixel art because that’s all I can reasonably attempt myself, I nevertheless want to give 3D a try. The other big reason to go with 3D is that I can build an animation system and animate characters once rather than 8x for the various viewing angles. I was wanting to build a skeletal animation system, but felt that 2D skeletal animation systems very easily feel flat without serious artistic effort.
The general image I have in my mind is a souls-like 2D platformer with movement and combat somewhat similar to playing Link in Super Smash, except with some additional movement mechanics like ladders and other climbable surfaces and no bubble shield. It’ll probably never be a full game but maybe I can make a proper level and boss at the end.
I’ll be using C++ and vscode for this, on Linux. I’ll try to minimize library use, but will leverage SDL2 as my platform library and probably OpenGL for 3D graphics. I love ImGui and will use that for dev UI.
What I tried first Didn’t Work
When I first started, I tried to go with an object system where the world is made of convex polygonal colliders. Seems reasonable:
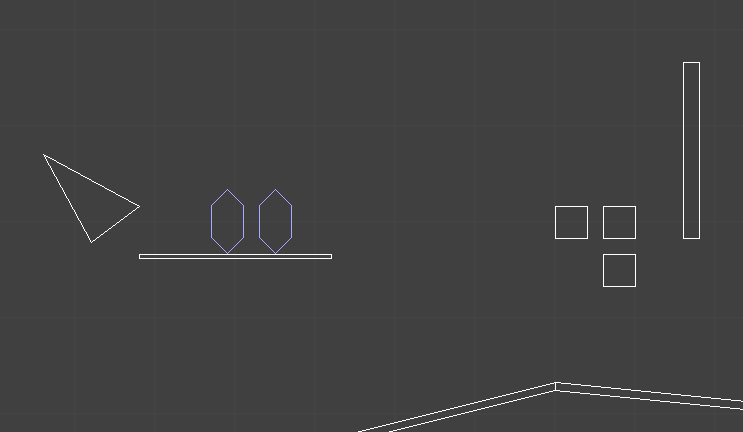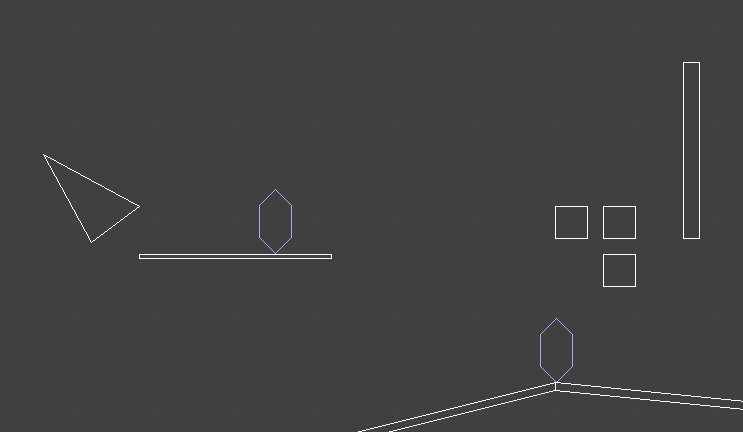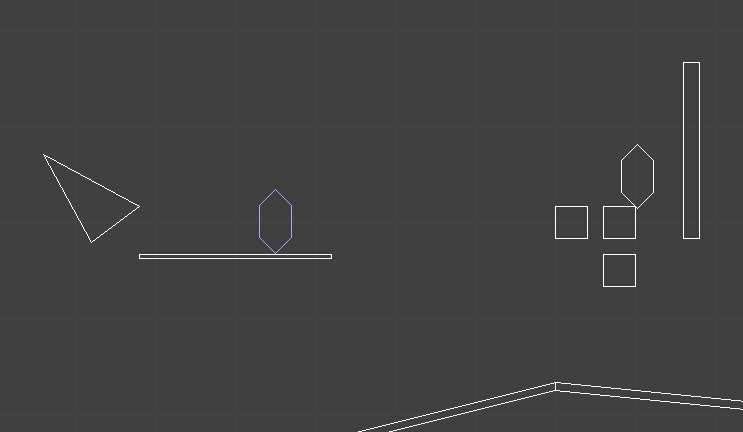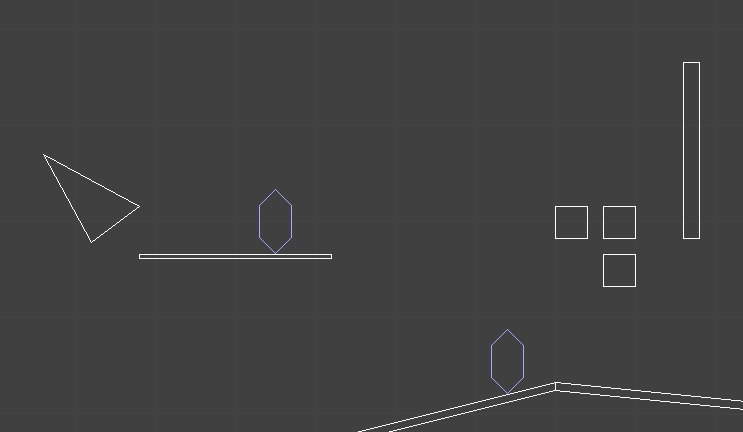
The player (and one enemy) have colliders represented by these six-sided shapes. The white polygons are static geometry. So far so good.
When an entity moves, it ticks forward by \(\Delta t\). I could have done this the boring way by:
- Moving the entity its full distance
- Checking for collisions
- Shunting the entity out of any colliding polygons
I’ve written about why this is a bad idea. In short, this approach can cause tunneling or other weird physics effects, especially when the entity is moving fast or when there are multiple intersecting bodies.
The system I implemented sought to instead find the first collision. This is the same as taking the source polygon and sweeping it along the direction of travel and finding the longest sweep \(\delta t \in [0, \Delta t]\) that does not intersect anything:
This sweeping method is harder to formulate. We aren’t really colliding the player’s collider with each static collider. Instead, we are colliding the swept player collider , but we still want to back out the maximum step we can take in our direction of motion. So we’re effectively sweeping the player collider along \(\Delta t \cdot \boldsymbol{v}\) and then checking for collisions, and we have to find the smallest \(\delta t\) such that the volume swept along \(\delta t \cdot \boldsymbol{v}\) does not collide.
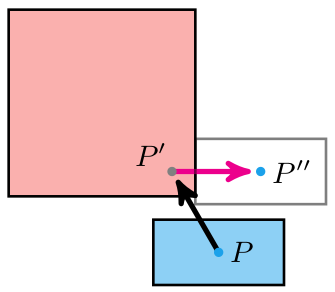
The way I implemented that was to fall back to our trusty strategy of using the . That is, we can expand the other polygon by the player’s collision volume first, and then all we have to do is check whether the line segment between the player’s starting location and that location shifted by \(\Delta t \cdot \boldsymbol{v}\) intersects with the polygon:
That mostly worked. It just has a lot of trouble with corner cases. For example, when the player is standing on a surface and we’re traveling along it. We don’t want floating point errors to accidentally place the player inside the supporting polygon. This was particularly problematic in the gameplay gif above, where the player ends up wedged between two squares and slides through one of them.
I had a lot of trouble with walking. I wanted the player to be able to walk across colliders along the floor without treating it like a ramp and launching off for a bit:
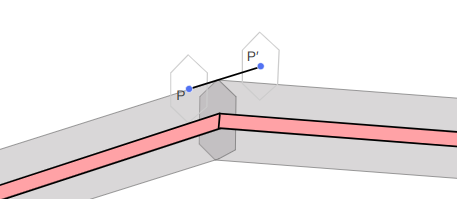
This means we have to do some hacky checks to figure out when we’re walking along a polygon and reach its end, and may need to transition to walking along a new polygon. I tried getting this all to work reliably, and got pretty far, but ultimately the number of hacks I had to add made the system untenable and left a bad taste in my mouth.
Redesign
The fundamental problem is that my previous system was fully continuous, but that continuity inherently had issues with floating point effects when the player is supported by geometry. In these cases, we want something more discrete that can concretely tell us which side of the geometry we are on. Furthermore, I wanted something that could more easily tell me whether, when walking along a surface, there was another surface to walk on after passing the end of the current segment. These thoughts lead me to the trusty Delaunay mesh data structure.
I’ve written blog posts that use constrained Delaunay meshes (aka DCELs) a few times now. Now that I know this data structure exists, I keep finding uses for it.
Delaunay meshes are triangle meshes in which we try to keep the triangles as equilateral as possible (to avoid very fractured / long and narrow tiles). Constrained Delaunay meshes are the same thing, except we force certain edges to exist. This makes these meshes useful for things like representing map geometry, where we force walls to be edges in the mesh:
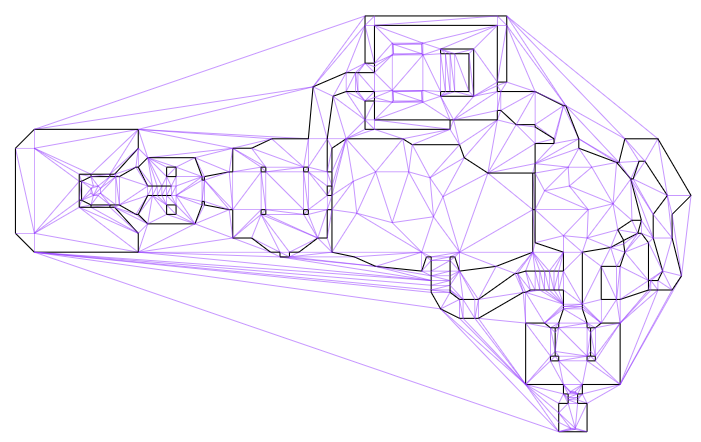
The E1M1 map from DOOM, after I’ve loaded it into a constrained Delaunay mesh
I actually advised that one use constrained Delaunay meshes for 2D player movement in this previous blog post. I hadn’t initially followed my own suggestion because the mesh is dependent on both the level geometry and the player collider (each polygon is expanded by the player collider via a Minkowski sum). If the player ducks and their collider shrinks, then we have to change our mesh. If an enemy has a different sized collider, then it should use a different mesh. If a piece of level geometry moves, such as a platform or door, then we need to change the mesh. All of these problems are still problems, but I’ll have to find workarounds for them. Nevertheless, I’m going with exactly what I spelled out in that earlier blog post.
My new plan was to keep track of both the player’s position and the triangle the collision mesh that they find themselves in. The collision mesh already accounts for the player’s collision volume, so we need only keep track of their center position. When they move, we check to see if their motion would take then out of their containing triangle, and if it does, we handle collisions (if necessary) at the crossed edge.
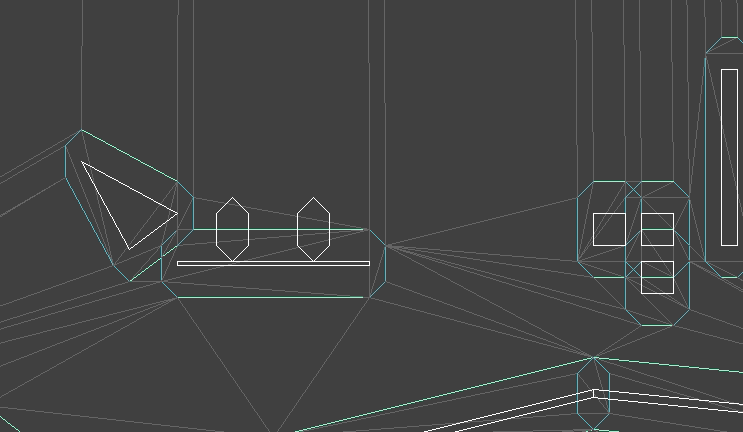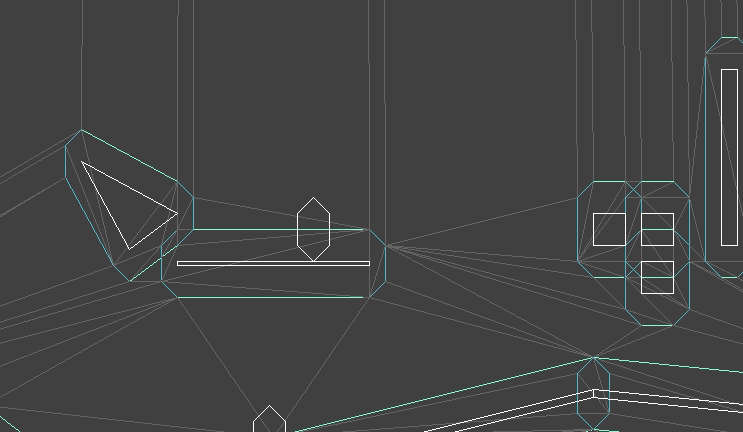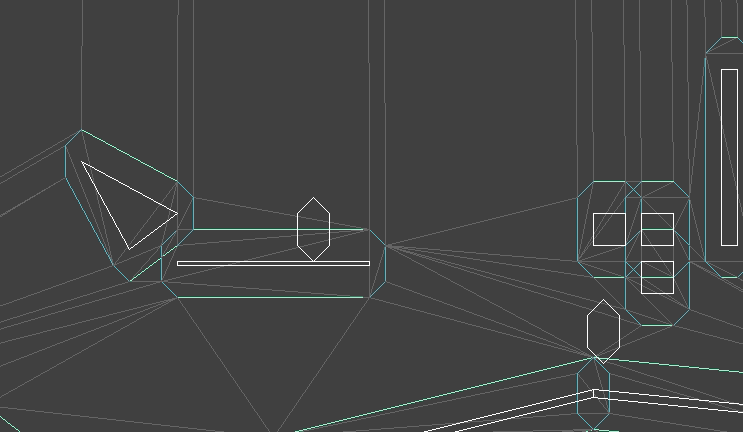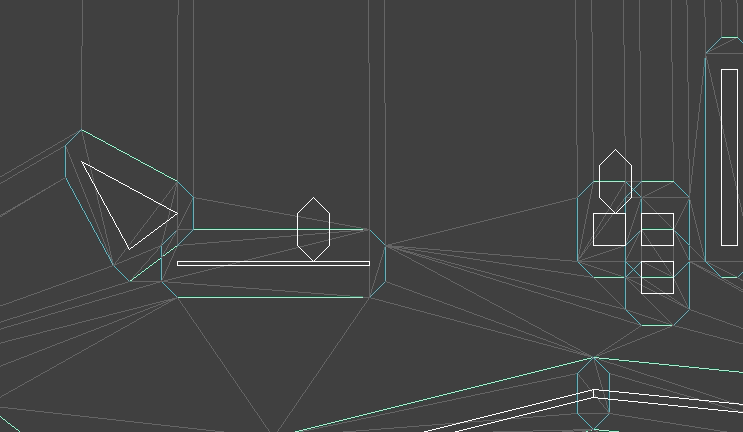
Here we see the updated system, along with the collision mesh.
Building the Mesh
Since I’ve covered how the movement works before, I’d rather focus on how we get the mesh.
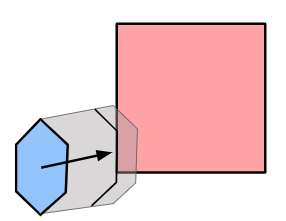
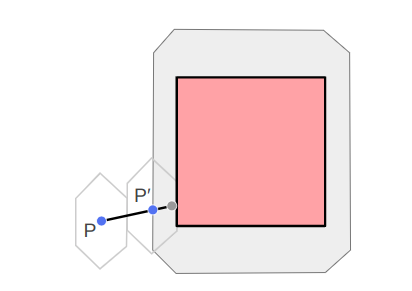
This mesh is obtained by expanding each polygon by the player’s collision volume, and then adding all resulting edges to the Delaunay mesh. These edges are constrained to ensure that they remain in the final mesh (otherwise, we might flip edges in order to make them more equilateral). The main difficulty arises in the fact that the edges of the expanded polygons may intersect, and we nevertheless have to support them in our final mesh:
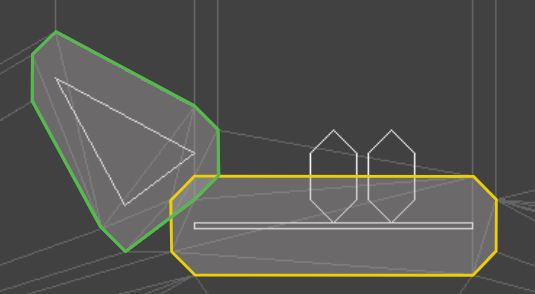
For example, these expanded polygons overlap.
I had previously tackled this using polygon unions via Clipper2. I could do that again, but want to avoid the loss of information that comes with replacing two or more overlapping polygons with a single polygon. For example, I might want to know which feature my player is standing on. For example, I may end up wanting to support removing objects. Plus, figuring out my own solution is a reward unto itself.
What I ended up doing was updating my method for constraining edges in a DCEL. During the development of TOOM, I had made it possible to load the DOOM level geometry and constrain the appropriate edges. Here we just added sides as we went, and constrained them after adding them:
for (Linedef linedef : linedefs) {
// Insert vertex a and b.
for (i16 i_vertex : {linedef.i_vertex_start, linedef.i_vertex_end}) {
const common::Vec2f& v = doom_vertices[i_vertex];
InsertVertexResult res = mesh.InsertVertex(v);
if (res.category == IN_FACE || res.category == ON_EDGE) {
mesh.EnforceLocallyDelaunay(res.i_qe);
vertex_indices[i_vertex] = mesh.GetVertexIndex(res.i_qe);
}
}
// Now ensure that there is a line between A and B.
// If there is not, flip edges until there is.
QuarterEdgeIndex qe_a =
mesh.GetQuarterEdge(vertex_indices[linedef.i_vertex_start]);
QuarterEdgeIndex qe_b =
mesh.GetQuarterEdge(vertex_indices[linedef.i_vertex_end]);
QuarterEdgeIndex qe_ab = mesh.EnforceEdge(qe_a, qe_b);
mesh.ConstrainEdge(qe_ab);
// sidedef and passability stuff...
}For example, we might add the vertices for A and B, and then end up with a mesh that is locally Delaunay but does not have an edge between A and B:
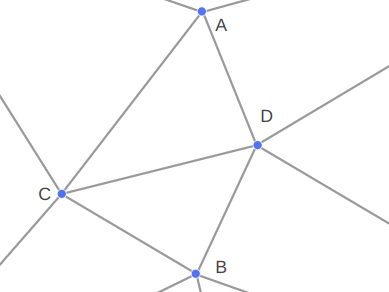
The call to EnforceEdge then flips CD in order to get the edge we want:
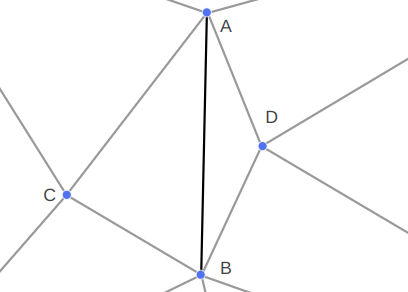
This approach worked for the DOOM maps because the sides there never crossed over one another. For example, if CD is another enforced edge, there was no way to also enforce AB by flipping edges:
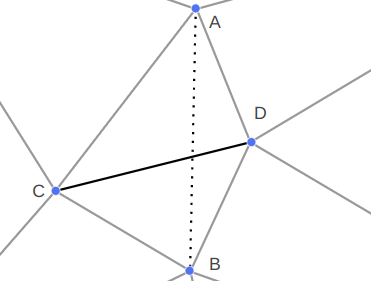
I needed a more general way to specify two points A and B and then adjust the mesh such that those two points are joined by a straight line, potentially via multiple colinear segments.
The updated algorithm has an outer loop that alternately tries tackling the problem from A to B and from B to A. As soon as it finds or produces a connection, it terminates. If it fails to make progress from both directions, it exits out.
Attempting to make progress from A to B starts by finding the edge from A that is as close as possible in a counter-clockwise / right-hand sense to the desired segment AB:
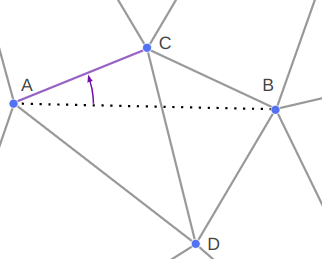
We’ll call the other side of this segment C. If C = B, we are done, as then AB already exists.
It is possible that C lies along AB. When this happens, we replace A with C and return to the outer loop:
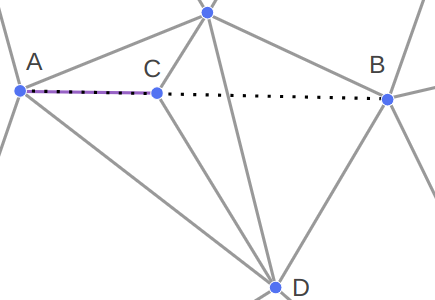
If we haven’t returned yet, then AC is counter-clockwise of AB. We need to flip CD, where D is on the other side of AB from C. If CD is not constrained, we can flip it.
The most interesting case occurs when CD is constrained. We cannot flip CD because it is fixed – we want it to remain an edge in the final mesh. So we instead introduce a new point E at the intersection of AB and CD, split CD at E, and add AE and EB:
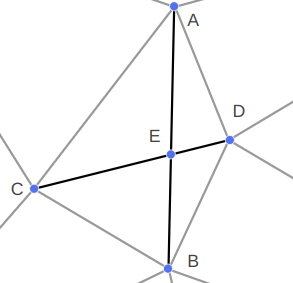
We can see this in action in the TOOM mesh editor, updated with this method:
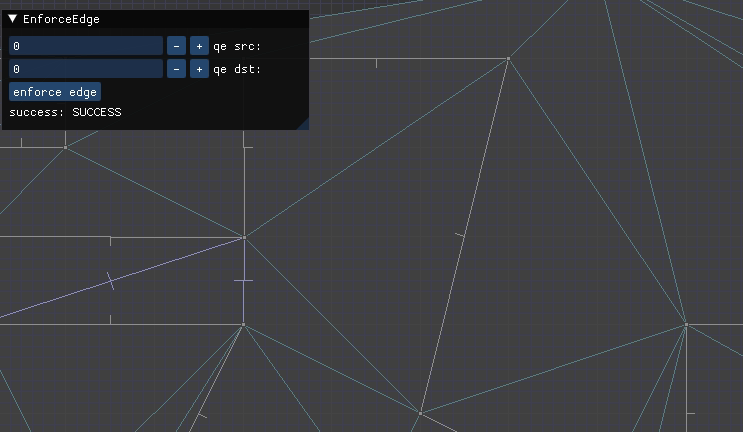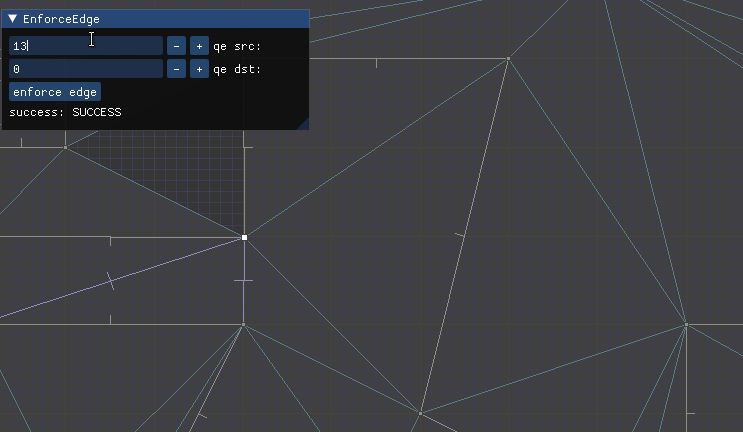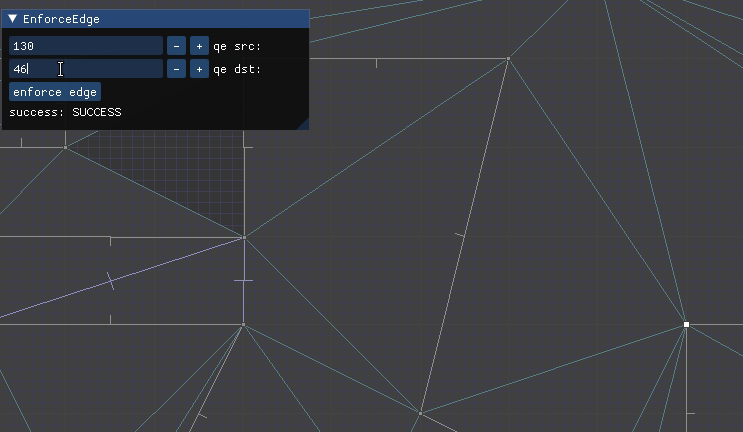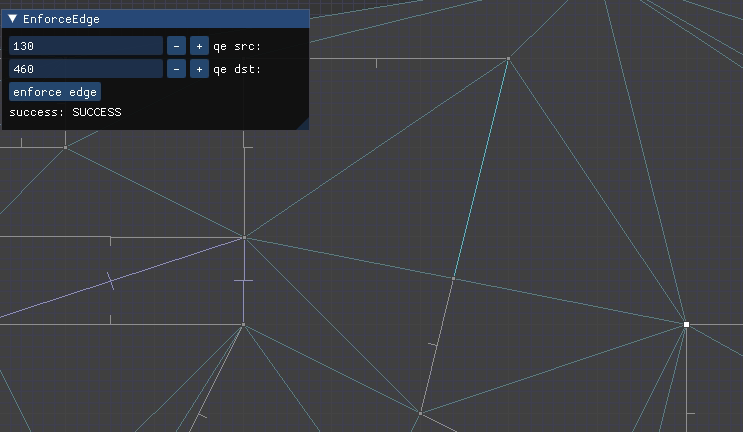
Here we have a constrained edge
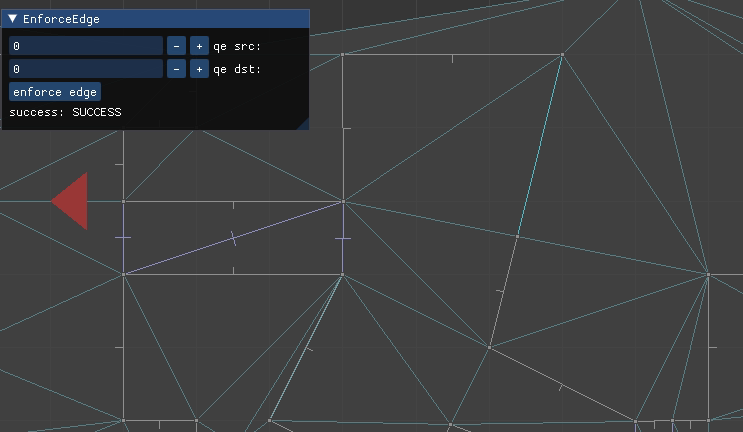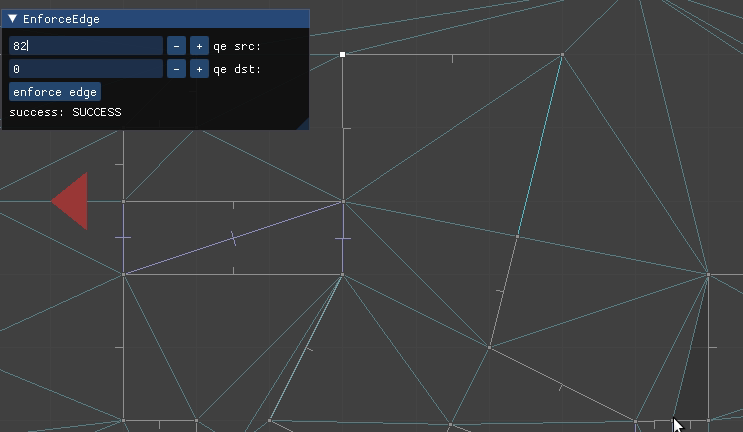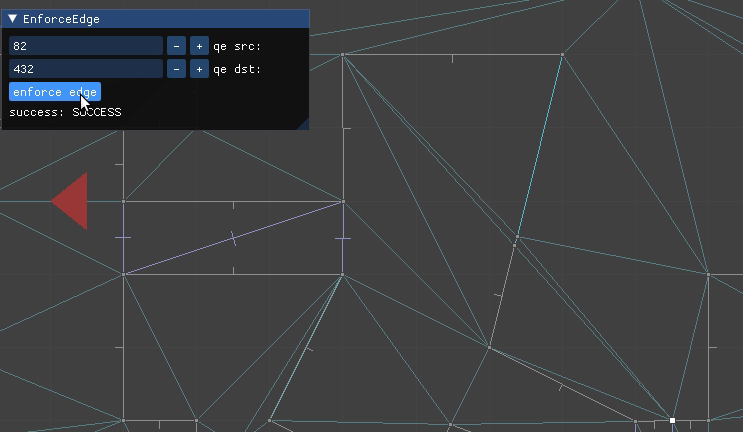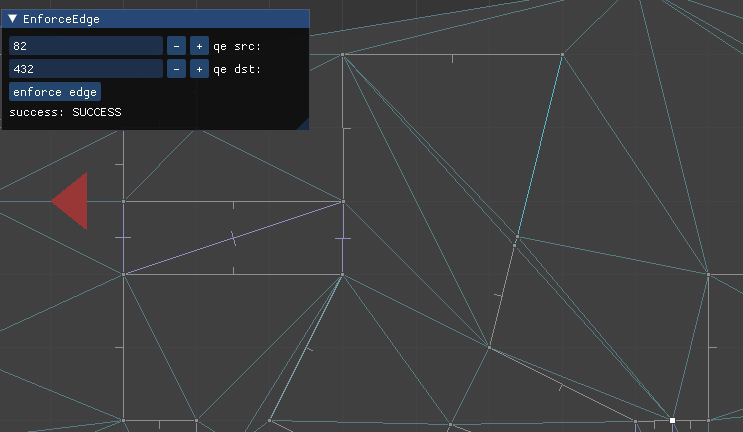
Here we have to flip or intersect multiple edges
So far I’m just building a mesh with constrained edges matching those of the expanded collision polygons, and only have a single such mesh to reflect the player’s collision polygon. I do not yet track which polygon corresponds to which triangle, nor do edges otherwise have any special properties. Nevertheless, what I have is sufficient for basic 2D player movement.
The player (and any other entity) has a 2D position and a triangle face in which their position lies. The 2D position is continuous, but the triangle face is discrete. Having something discrete resolves the issue with floating point rounding – we know exactly which side of a line we are (supposed to be) on.
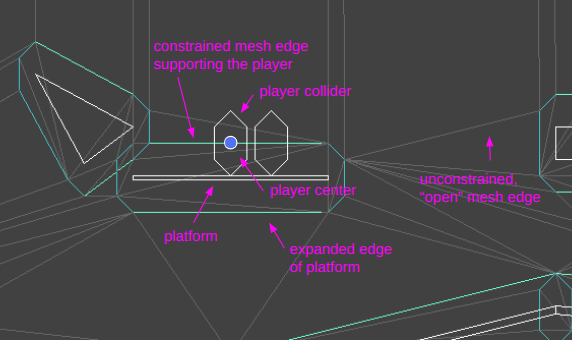
Note that the constrained Delaunay mesh does not actually contain the white collider polygons:
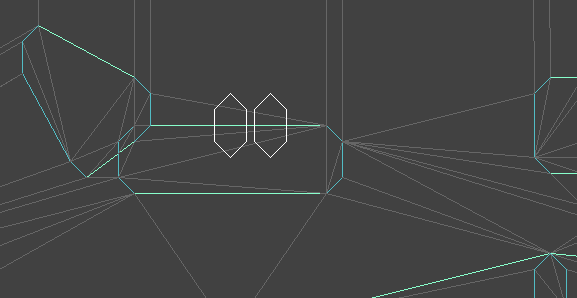
I’ll probably talk about this more next time, but movement physics currently get processed in two different ways. If the moving entity is airborne, then they move according to . If we collide with a solid edge, we lose all velocity going into it and then continue on in our new direction. Colliding with a solid edge can result in the agent transitioning to the supported state.
If the moving entity is standing or walking on a surface, i.e. is supported, we handle things a bit differently. Here their velocity is projected along the supporting surface. Any time they move past the end of the supporting surface, we find the next supporting edge (if there is one) and allow them to transition over. If they are moving fast enough or there is no supporting edge to connect to, they transition to being airborne.
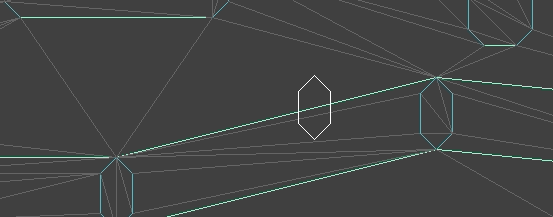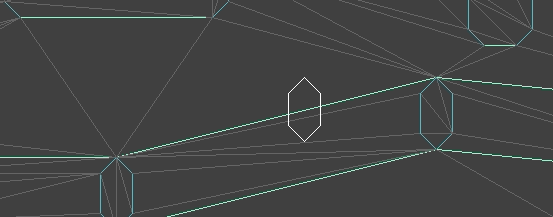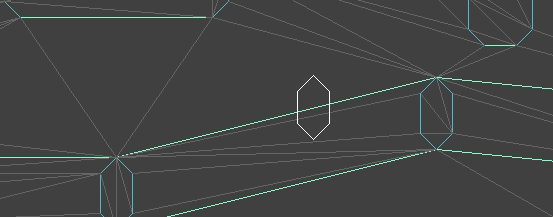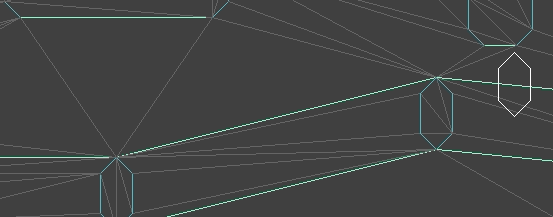
The player walking across supporting surfaces
Conclusion
Constrained Delaunay meshes resolved many of the tricky issues that arose with tackling 2D player movement for arbitrary terrain geometry. Knowing which face a player is in is a discrete fact that removes the issues with numeric imprecision in general polygon-on-polygon collisions, without having to resort to shunting. It also naturally allows us to leverage the mesh to query things like the next supporting face.
The code for the updated Delaunay mesh is available here.
In the future I hope to support additional motion states, such as climbing on ladders and surfaces. I’ll want to add support for dropping down “through” a platform, wall slides and jumps, and some other basic sidescroller movement features. I want to add 3D GPU graphics, and with that, animations and combat. It turns out there is a lot that goes into a basic game.