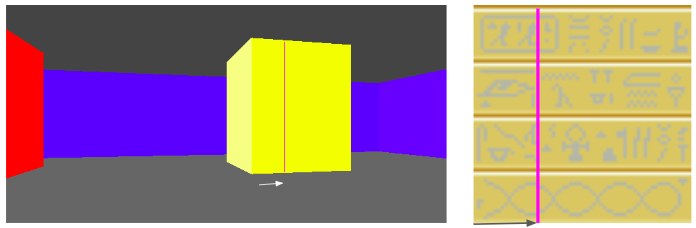
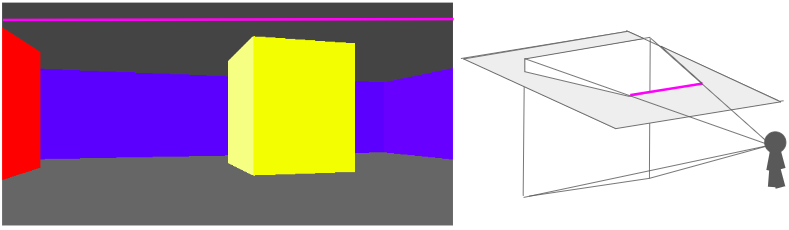
I’ve continued tinkering with my little C software renderer covered in previous blog posts. So far we’ve rendered a blocky, textured environment reminiscent of Wolfenstein 3D:

You’ll notice from the window header that the project is called TOOM, as in, Tim DOOM. It isn’t Timenstein 3D, so we have some work to do.
In this blog post we’ll go off-grid and move to general 2D geometry.
Binary Space Partitioning
John Carmack’s great innovation in creating DOOM, the design change that made rendering general 2D geometry in a constrained computing environment possible, was the BSP tree. BSP trees make it efficient to walk over the surfaces in your world in a front-to-back order, based on the camera location.
Each node in the tree represents a splitting plane (or line, rather, as this is 2D) that subdivides the level. All faces below that node lie entirely on one or the other side of that dividing line. At the bottom of the tree you get leaf nodes, which each represent a single convex map region:
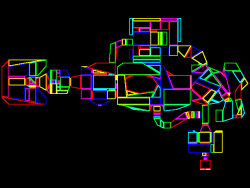
DOOM’s E1M1 map, image from the doomwiki
While the BSP tree is a genius addition, it does come with its disadvantages. The main one being its construction. For DOOM this meant running Node Builder after level design, a process that does a lot of iteration to find the best splitting planes for a well-balanced tree. Not only does this take a while, it also requires the level geometry to remain static. This means no 2D geometry changes. (DOOM’s doors all move vertically).
I kind of want to be able to support geometry changes. Plus, I kind of like the idea of figuring out something different. So, we’re going to take another approach.
Keep on Raycasting
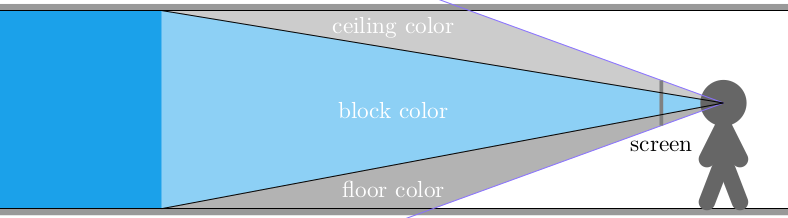
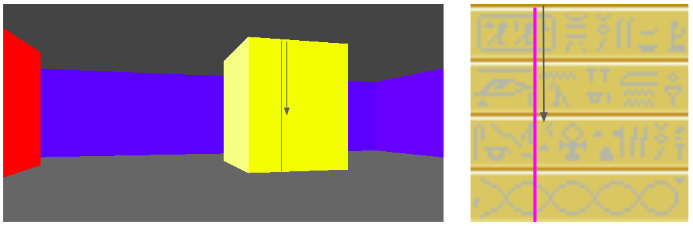
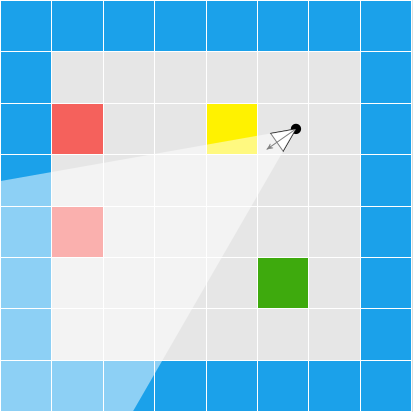
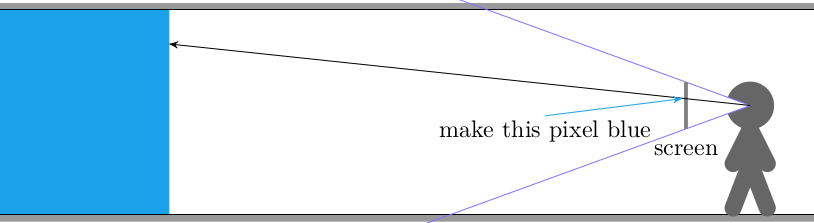
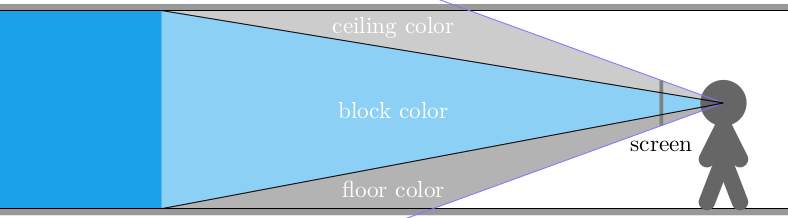
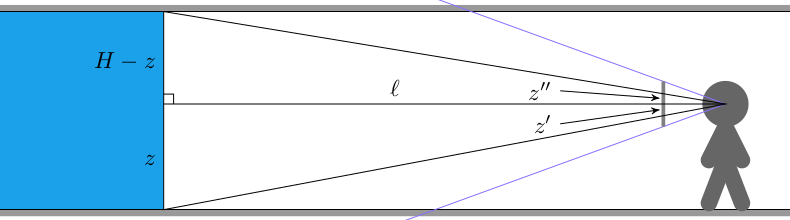
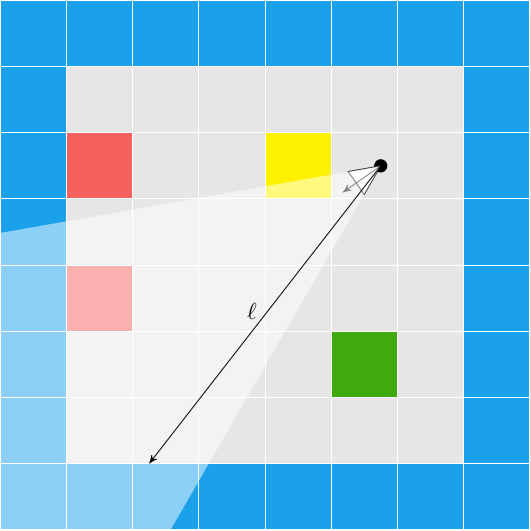
In Wolfenstein Raycasting in C, we talked about how the software renderer casts rays out into the world for every pixel column in the screen:

This raycasting was fairly efficient because we limited our geometry to a regular grid:
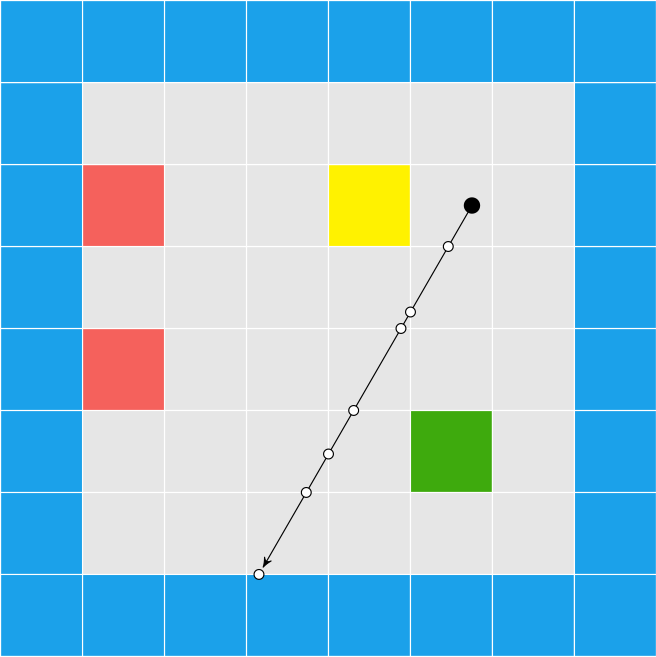
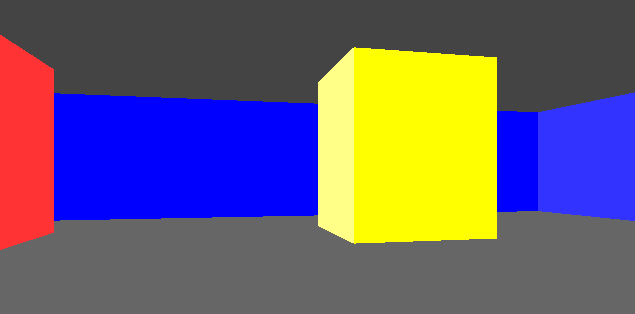
Now, we’re going to do the exact same thing, except on a triangle mesh:
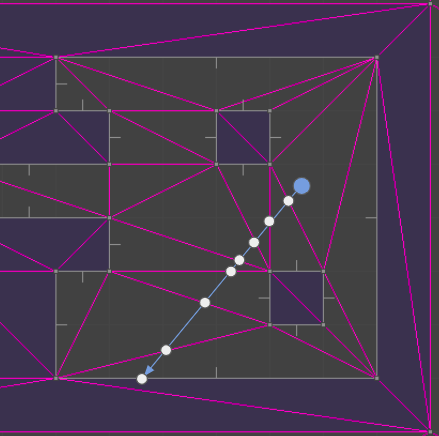
Moving to a triangle mesh has several consequences. On the plus side, it supports general 2D geometry, so we no longer have to constrain ourselves to a grid of blocks. We can fairly easily move vertices and mutate our environment. On the other hand, casting a ray through a set of triangles tends to be more computationally expensive, we have to develop and maintain a more complicated data structure, and we aren’t entirely free to mutate our environment – our triangles have to remain valid (right-handed).
It isn’t 1993 anymore, so I’m hoping that the performance hit from raycasting on a mesh isn’t too bad on a modern processor. I’ve already been tinkering with triangle meshes, so I’m eager to adapt what I learned there to this new application. I also think we can overcome the editing limitations.
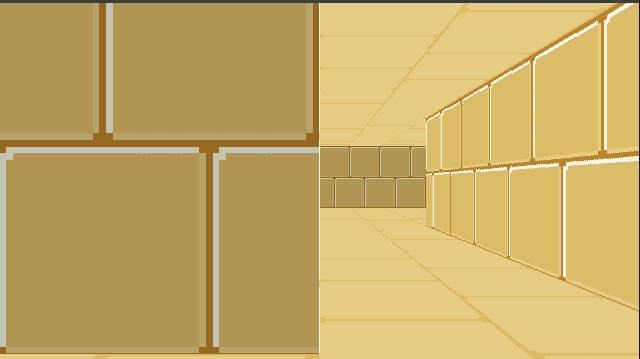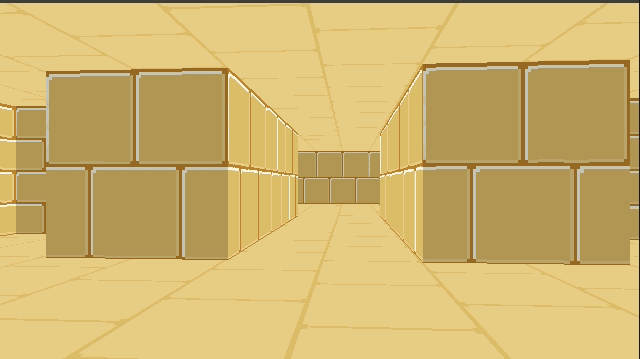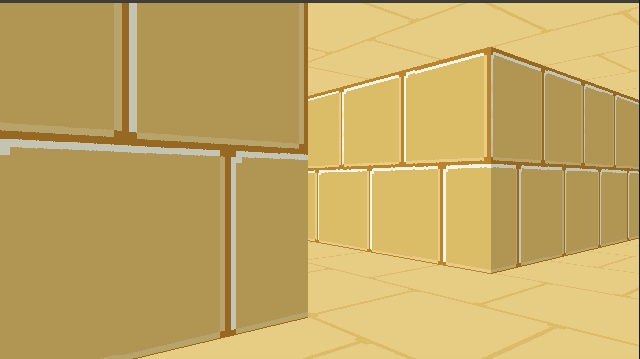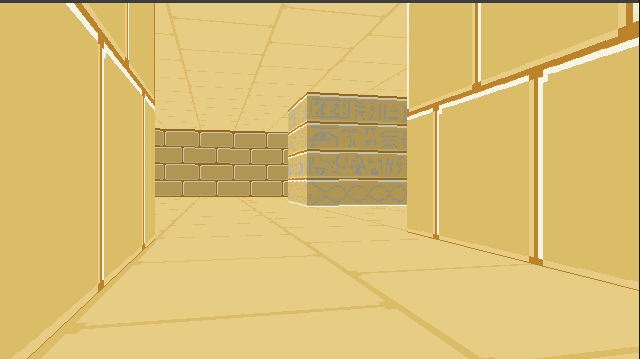
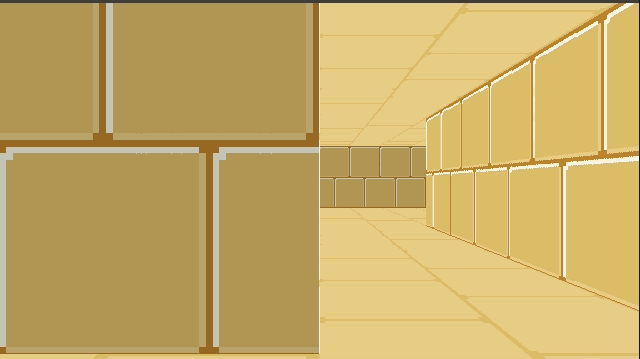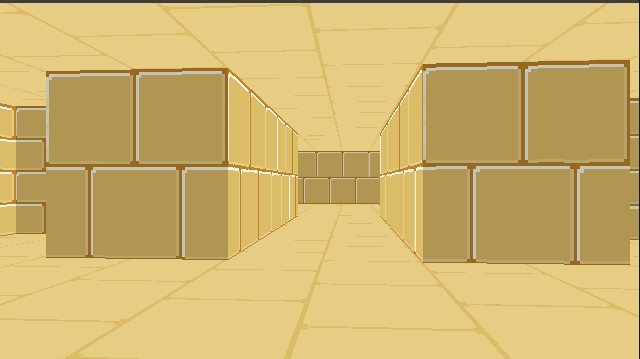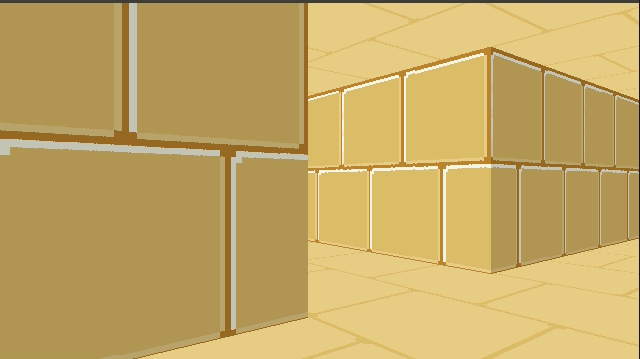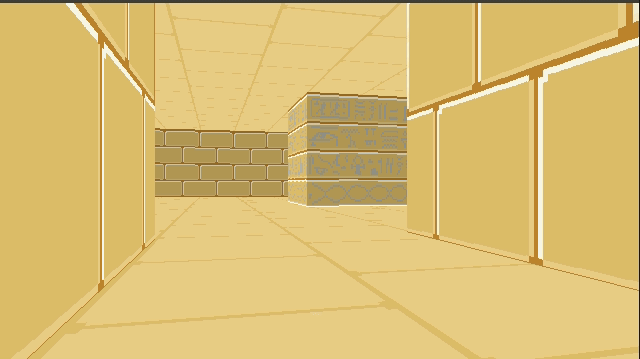
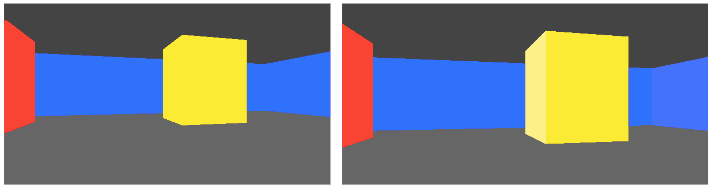
Below is a GIF from TOOM. The left half of the image is rendered with the new triangle meshes. The right half of the image is rendered with the old blocky technique. (The new map was made to be identical to the old one, for now). The textures assigned to the walls aren’t the same just yet, so you can see a fairly clear division.

The debug view gives us a better sense of what is going on:

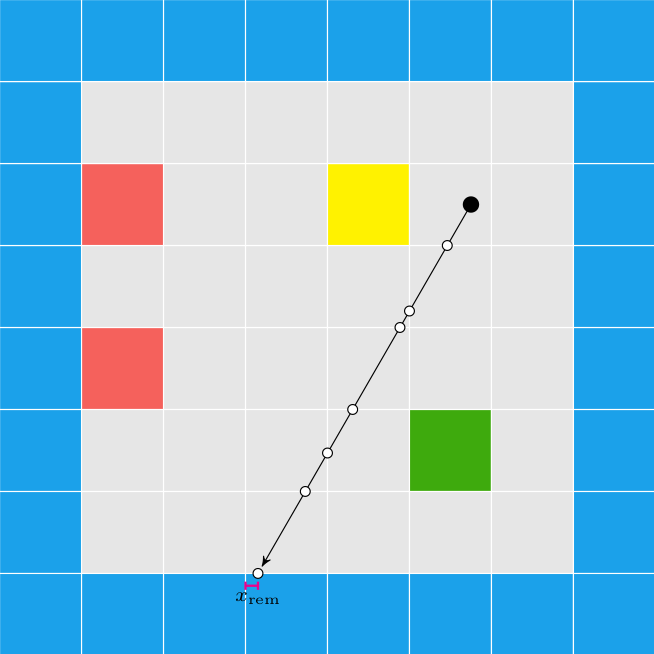
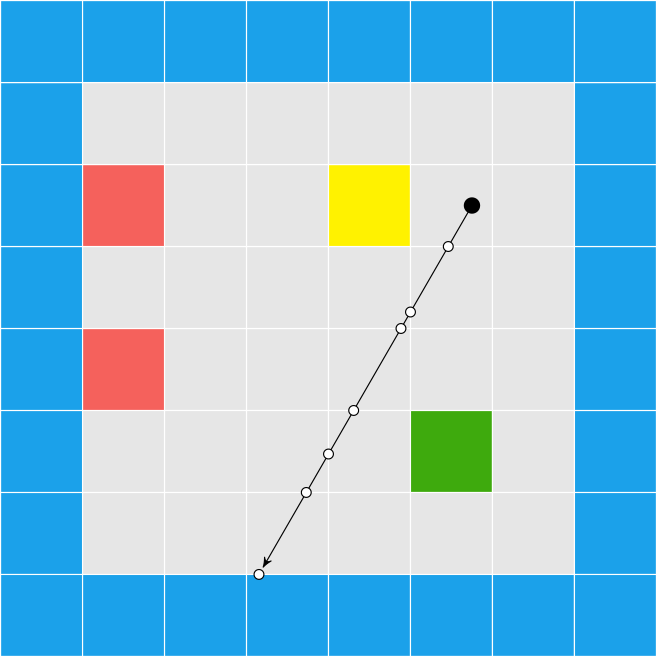
Raycasting through triangles is the same, conceptually, as raycasting through a grid. We keep casting through cells until we reach a solid cell. Now, instead of square cells with regular spacing, we have arbitrarily-sized, triangular cells.
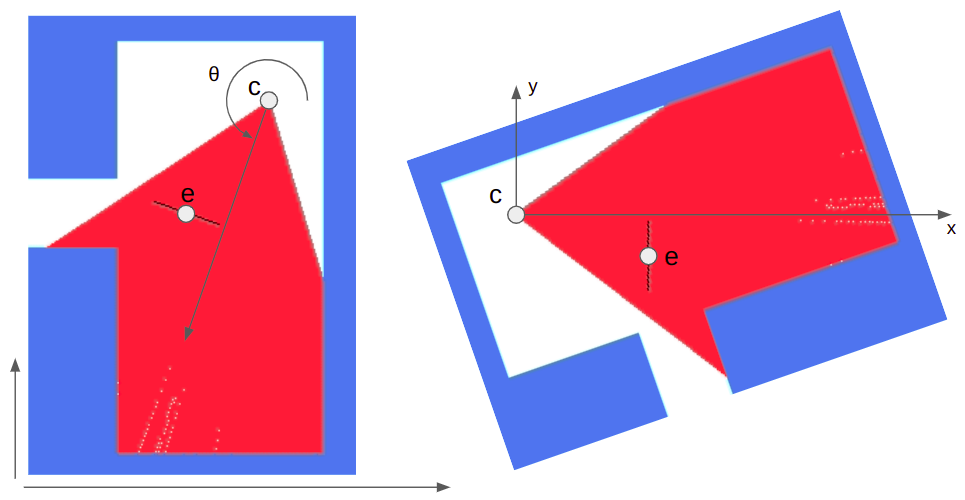
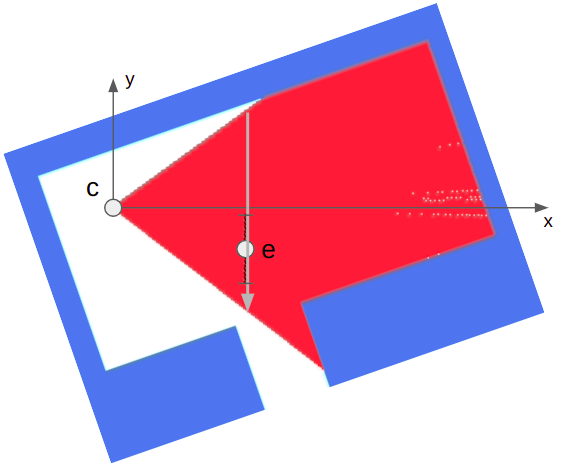
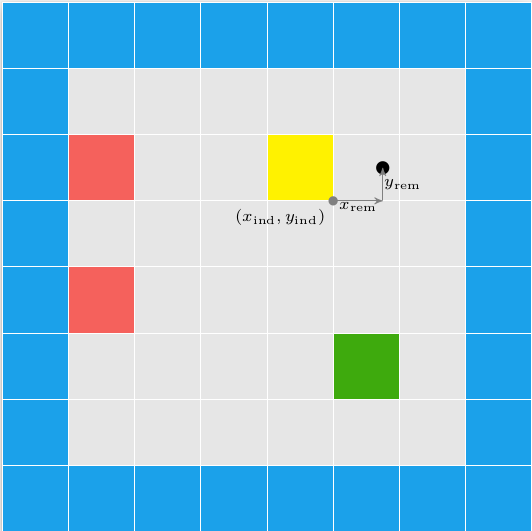
Each raycast starts with a ray at the camera location \(\boldsymbol{p}\) heading in a direction \(\hat{\boldsymbol{d}}\). As we iterate \(\boldsymbol{p}\) will be shifted out into the world. In the first iteration, \(\boldsymbol{p}\) will be the camera location and can lie inside a triangle face. In future iterations, \(\boldsymbol{p}\) is lies on an edge that we crossed in the previous iteration.
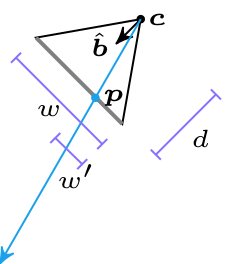
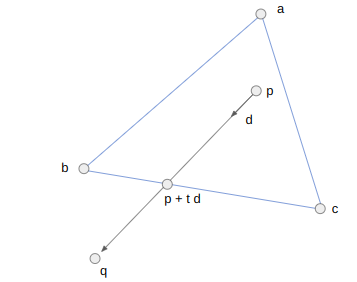
We take the three bounding vertices \(\boldsymbol{a}\), \(\boldsymbol{b}\), and \(\boldsymbol{c}\) and intersect the line through \(\boldsymbol{p}\) with the direction \(\hat{\boldsymbol{d}}\) with AB, BC, and CA, representing each intersection point as \(\boldsymbol{p}’ = \boldsymbol{p} + t \hat{\boldsymbol{d}}\). We step forward to the edge that we hit first. That is, the edge for which \(t\) is smallest (but positive). We ignore any edge we are already on.
We start by computing \(\boldsymbol{q}\), a point far enough along \(\boldsymbol{d}\) that it should exit the triangle:
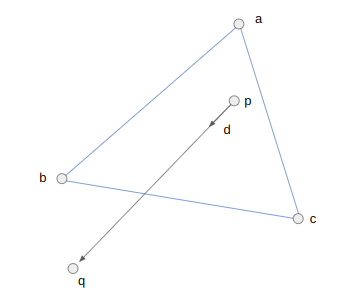
Before we calculate an intercept, we can disregard checking an edge EF if the triangle EFQ is not left-handed. This helps us avoid cases where an intersection will either never occur or lie behind our ray. For example, we can skip checking AB because ABQ is right-handed (counter-clockwise):
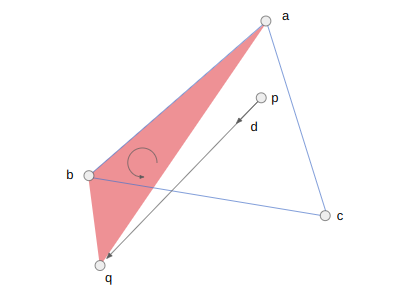
We should check BC, because the triangle BCQ is left-handed (clockwise):
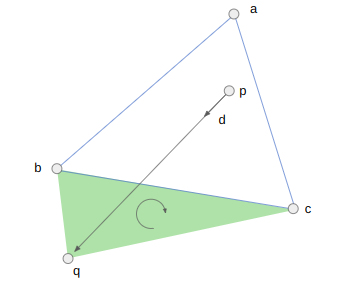
We can now calculate the interection point’s \(t\)-value. For the edge BC, this is:
\[t_{BC} = \frac{(\boldsymbol{c}-\boldsymbol{b}) \times (\boldsymbol{p}-\boldsymbol{b})}{(\boldsymbol{q}-\boldsymbol{p}) \times (\boldsymbol{c}-\boldsymbol{b})}\]
In code, this works out to:
if (GetRightHandedness(b, c, q) < -eps) {
// We would cross BC
v2 v = c - b;
v2 w = p - b;
f32 t_bc = cross(v, w) / cross(q - p, v);
if (t_bc < t_min) {
t_min = t_bc;
qe_side = qe_bc;
v_face = v;
}
}We just repeat this block three times, once for each edge. Each time we get an intersection, we keep it if it is earlier than any previous intersection. When we do, we also store the edge that we pass over (via its quarter edge in the DCEL).
Just like before, we propagate our point \(\boldsymbol{p}\) up to the new edge and then either iterate again if the new face is empty, or break out if the new face is solid.
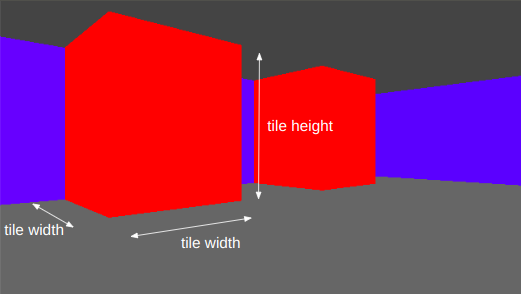
We do have to make some minor modifications in how we access the face texture. With the grid we could safely assume that every wall was square, with a corresponding 64×64 pixel texture. Now walls can have arbitrary aspect ratios, so we have to do a tiny bit of math to index into the texture based on our intersection location along the edge:
f32 PIX_PER_DISTANCE = TEXTURE_SIZE / TILE_WIDTH;
QuarterEdge *qe_face_src = qe_dual->rot->rot->rot;
f32 x_along_texture = length(v_face) - length(pos - qe_face_src->vertex);
u32 texture_x = (int)(PIX_PER_DISTANCE * x_along_texture) % TEXTURE_SIZE;Collision Detection
One immediate advantage of using the DCEL is that we can leverage it for collision detection. In DOOM, collision detection is done via a blockmap, which is just a discrete 128×128 pixel grid. Each grid cell stores the lines in that block. An entity moving in a cell can just check for collision against all of the lines in the cell. The blockmap is constructed on level export, and again assumes static 2D geometry.
We don’t have to use a bockmap, because we have the DCEL. We can simply store the face that our player is in and check for collisions every time we move them. Our player movement code is the same as the player movement code in this previous blog post. Any time we would cross over a solid edge between two faces, we simply move up to the edge instead, and lose any velocity into the edge.
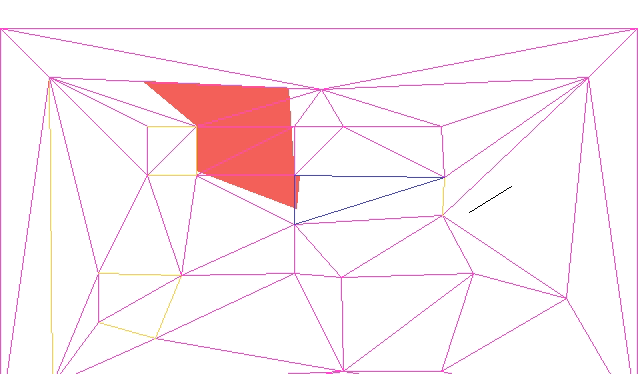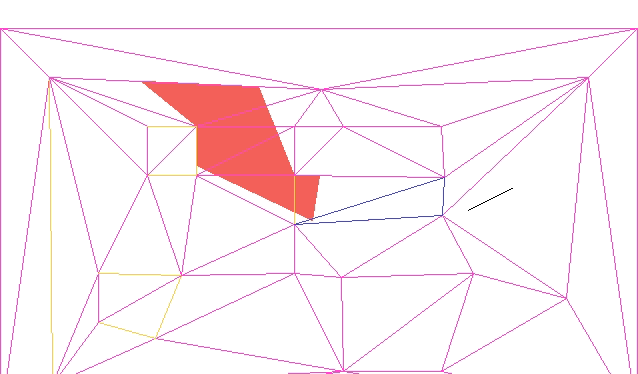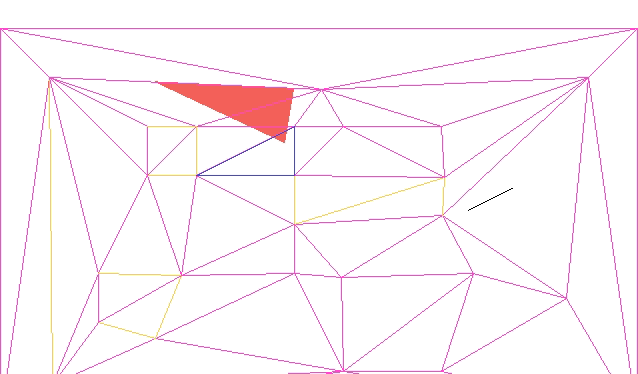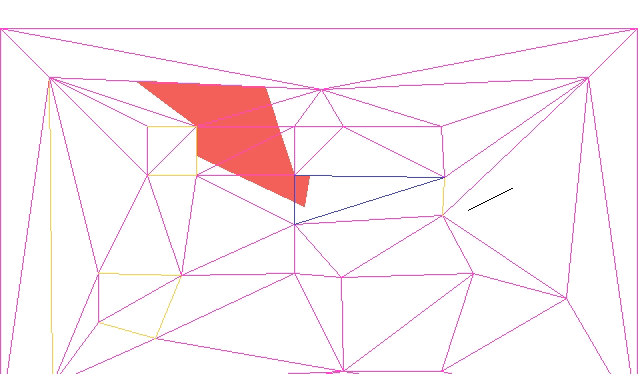
The current approach assumes the player is a single point. If we want, we can create a second collision mesh that uses inflated solid geometry to compensate for the player’s collision volume. We would have to keep that second mesh synchronized with any changes to the geometry mesh.
DCELs make pathing and shooting computations easy too. DCELs are primarily used in games for pathing (via Nav Meshes) and collision checking for a gunshot is just a raycast where we also care about intersections with enemies.
Game Map Representation
The biggest difference here was not so much the rendering code, but more the integration of the mesh data structure and how we represent the game map. With the Wolfenstein-style renderer we were able to represent the map using 2D arrays:
tiles = UInt8[
1 1 1 1 1 1 1 1 2 1 1 1 2;
1 0 0 0 0 0 0 1 2 0 0 0 2;
1 0 0 3 0 0 2 2 2 0 0 0 2;
1 0 0 0 0 0 0 0 0 0 0 0 2;
1 0 0 0 0 0 2 2 2 0 0 0 2;
1 0 2 0 0 0 0 1 2 0 0 0 2;
1 0 0 0 0 0 0 1 2 0 0 0 2;
1 1 1 1 1 1 1 1 2 3 3 3 2]
floor = UInt8[
1 1 1 1 1 1 1 1 2 1 1 1 2;
1 4 4 4 4 4 4 1 2 5 5 5 2;
1 4 4 3 4 4 2 2 2 5 5 5 2;
1 4 4 4 4 4 2 2 2 5 5 5 2;
1 4 4 4 4 4 2 2 2 5 5 5 2;
1 4 2 4 4 4 4 1 2 5 5 5 2;
1 4 4 4 4 4 4 1 2 5 5 5 2;
1 1 1 1 1 1 1 1 2 3 3 3 2]
ceiling = UInt8[
1 1 1 1 1 1 1 1 2 1 1 1 2;
1 4 4 4 4 4 4 1 2 4 4 4 2;
1 4 4 3 4 4 2 2 2 4 4 4 2;
1 4 4 4 4 4 2 2 2 4 4 4 2;
1 4 4 4 4 4 2 2 2 4 4 4 2;
1 4 2 4 4 4 4 1 2 4 4 4 2;
1 4 4 4 4 4 4 1 2 4 4 4 2;
1 1 1 1 1 1 1 1 2 3 3 3 2]Each cell could thus be marked as solid or not depending on whether the cell’s entry in tiles is 0. Nonzero values corresponded to texture indices. Similar arrays were used for the floor and ceiling textures.
With the general 2D geometry, we no longer have a convenient text short-hand. The DCEL has a lot of pointers and is no fun to edit manually. We have to store all vertices, quarter edges, and the associations between them. We then optionally mark edges as being solid, and when we do, set edge texture information.
At this point the game map consists of two things:
- a triangle mesh
- optional side information
My representation for side information is pretty simple. It is just a structure with some flags, a texture id, texture x and y offsets, and the associated quarter edge:
// The information associated with one side of an edge between vertices in
// the map. If this represents the directed edge A->B, then it describes the
// edge viewed on the right side of A->B.
struct SideInfo {
u16 flags;
u16 texture_id;
i16 x_offset;
i16 y_offset;
QuarterEdgeIndex qe;
};The map data is packed into the binary assets blob (similar to a DOOM WAD file) and loaded by the game at start.
Editing this game data is rather hard to do by hand, so I started working on an editor on the side. The editor is written in C++, and I allow myself the use of whatever libraries I want. I might go over that in more detail in a future post, but for now I just want to show how it can be used to adjust the map:
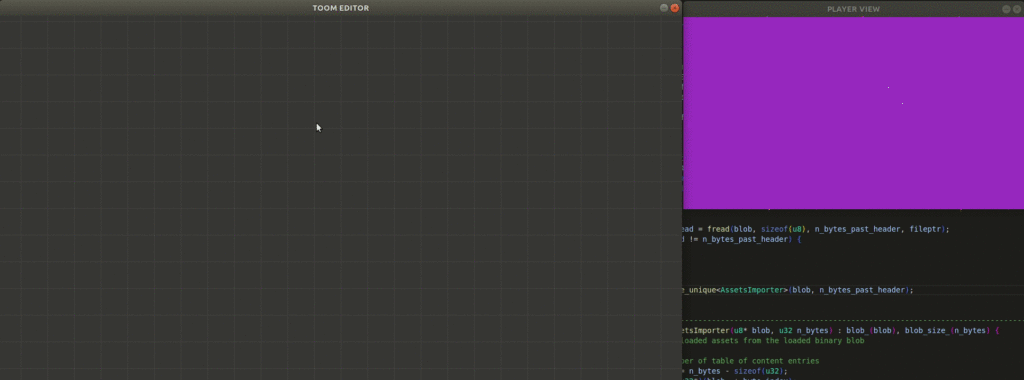
The gif here is fairly large. It may have to be viewed separately.
Having an editors gives us a place to put supporting code and lets us use more convenient data structures that aren’t streamlined for the C software renderer. The editor can then do the lifting required to export our game data into the form expected by the game.
Conclusion
The TOOM source code for this post is available here. I have been overwriting my assets file, and the new ones are no longer compatible, so unfortunately do not have a good assets file to share.
In this post we took our blocky Wolfenstein-style environment and moved to general 2D geometry. We didn’t follow DOOM and use a BSP, but instead stuck with raycasting and used a DCEL.
What we have now is much closer to DOOM, but still lacks a few things. Geometrically, we don’t have variable floor heights, which means we also don’t yet worry about wall surfaces between variable floor heights. We also aren’t animating doors or elevators, and we don’t have textures with transparency. We aren’t doing any lighting, other than manually setting some faces to be darker. DOOM really was groundbreaking.