Category Archives: optimization

Differential Evolution

by

Algorithms for Optimization covers Differential Evolution in its chapter on population methods. It is fairly easy to specify what it does, but the combination of things it does is somewhat strange, and it isn’t all that obvious why it would work, or work particularly well. That being said, there is plenty of support for Differential Evolution in the literature, so I figured there probably is a method to this method’s madness. We’re in the process of updating the textbook for a 2nd edition, so in this post I’ll spend some time trying to build more intuition behind Differential Evolution to better present it in the text.

The Algorithm

Differential Evolution is a derivative-free population method. This means that instead of iteratively improving a single design, it iteratively improves a bunch of designs, and doesn’t need the gradient to do so. The individual updates make use of other individuals in the population. An effective population method will tend to converge its individuals on the (best) local minima of the objective function.

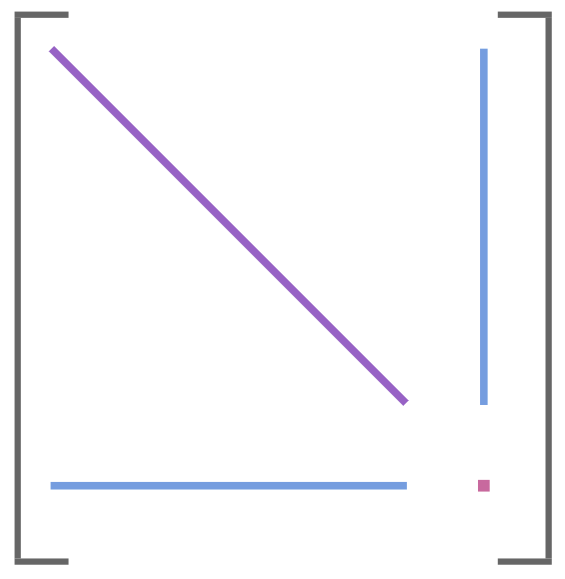
Differential Evolution applied to the Ackley function, proceeding left to right and top to bottom. Image from Algorithms for Optimization published by the MIT Press.

In each iteration, a new candidate individual \(\boldsymbol{x}’\) is created for every individual \(\boldsymbol{x}\) of the population. If the new candidate individual has a lower objective function value, it will replace the original individual in the next generation.

We first construct an interim individual \(\boldsymbol{z}\) using three randomly sampled and distinct other population members:

\[\boldsymbol{z} = \boldsymbol{a} + w \cdot (\boldsymbol{b} – \boldsymbol{c})\]

where \(w\) is a scalar weight.

The candidate design \(\boldsymbol{x}’\) is created via uniform crossover between \(\boldsymbol{z}\) and \(\boldsymbol{x}\), which just means that each component has a probability \(p\) of coming from \(\boldsymbol{z}\) and otherwise comes from \(\boldsymbol{x}\).

This is really easy to code up:

function diff_evo_step!(
    population, # vector of designs
    f,          # objective function
    p,          # crossover probability
    w)          # differential weight

    n, m = length(population[1]), length(population)
    for x in population
        a, b, c = sample(population, 3, replace=false)
        z = a + w*(b-c)
        x′ = x + (rand(m) .< p).*(z - x)
        if f(x′) < f(x)
            x[:] = x′
        end
    end
    return population
end

What I presented above is a slight simplification to the normal way Differential Evolution is typically shown. First, while my implementation samples three distinct members of the population for \(\boldsymbol{a}\), \(\boldsymbol{b}\), and \(\boldsymbol{c}\), it does not guarantee that they are distinct from \(\boldsymbol{x}\). They will pretty much always be distinct from \(\boldsymbol{x}\) for sufficiently large population sizes, and if not it isn’t all that detrimental.

Second, the standard way to define Differential Evolution always forces at least one component to mutate. This isn’t important if the crossover probability is large enough in comparison to the number of components, but in practice users have found that a very low, or even zero, crossover probability with one guaranteed mutation works best for many objective functions.

What is Going On

Differential Evolution is weird. Or at the very least, its unintuitive. Let’s break it down.

The algorithm proceeds by replacing individuals with new candidate individuals if they are better. So far so good.

The candidate individuals are formed by three things:

  • a baseline individual \(\boldsymbol{a}\)
  • a perturbation formed by the difference \(w\cdot(\boldsymbol{b} – \boldsymbol{c})\)
  • uniform crossover

Differential Evolution gets its name from the second bullet – the difference between individuals. This is its secret sauce. Its nice in that it provides a natural way to take larger steps at the start, when the population is really spread out and hasn’t found local minima, and smaller steps later on when the population is concentrated around a few specific regions:

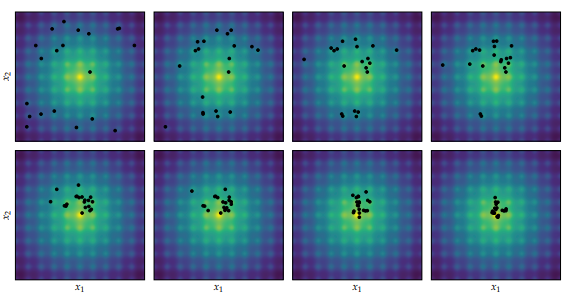
We can run a version of Differential Evolution that only has this differential, using \(\boldsymbol{x}’ = \boldsymbol{a} + w \cdot (\boldsymbol{b} – \boldsymbol{c})\). If we do that, we’ll get design improvements, but they’ll be local to the current individual. Including the baseline individual is going to do better:

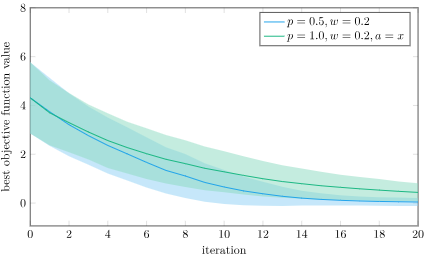
The mean best objective function value and 1 standard deviation intervals using Differential Evolution and pure differential on the Ackley function, over 1000 trials. I’m using \(w = 0.2\) to exaggerate the effect.

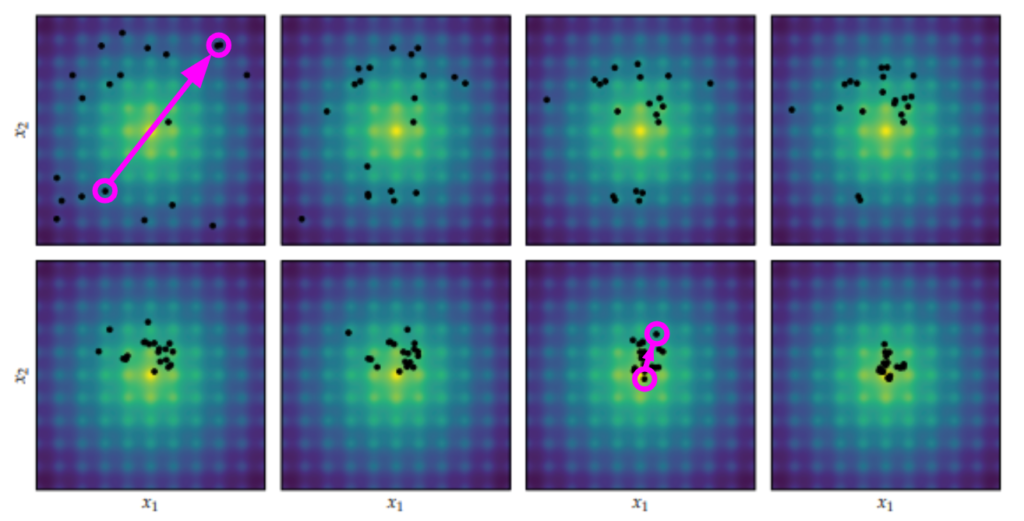
Local perturbations alone are often insufficient to get individuals out of local minima to better local minima. This is where the baseline individual \(\boldsymbol{a}\) comes in. Perturbing off of a different individual than \(\boldsymbol{x}\) means we could be substituting \(\boldsymbol{x}\) with a perturbed individual in a better local minima. When that happens, we’re basically warping \(\boldsymbol{x}\) to that better minima:

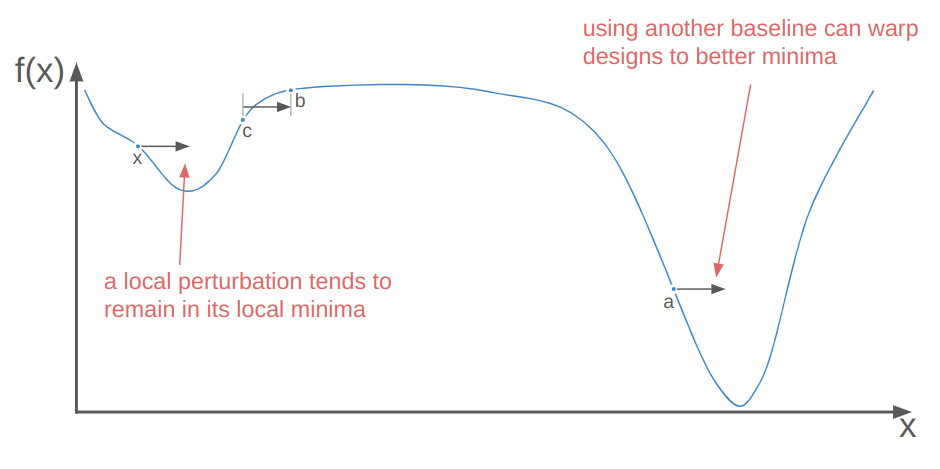
So that’s where \(\boldsymbol{a} + w \cdot (\boldsymbol{b} – \boldsymbol{c})\) comes from. What about uniform crossover? Let’s run an experiment.

Below I show the average and \(\pm 1\) standard deviation on the best objective function value vs. iteration for 1000 trials on a bunch of different algorithm variations on the Ackley function:

  • no perturbation (p=0.5, w=0.0)
  • no baseline individual (p=0.5, w=0.5, a=x)
  • baseline Differential Evolution (p=0.5, w=0.5)
  • high mutation rate (p=0.9, w=0.5)
  • guaranteed crossover (p=1.0, w=0.5)

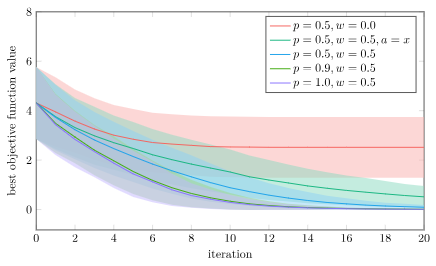
Without perturbations (w=0.0) we can’t really explore the space. We’re only looking at coordinate values that exist in our initial population. Its no surprise that that one does poorly.

Using just the baseline individual is the next-worst, because that one can’t as effectively jump individuals to new regions.

The top three performers are all Differential Evolution with varying mutation rates. We find that higher mutation rates in uniform crossover perform best. In fact, our best performance doesn’t use crossover at all, but just directly uses \(\boldsymbol{x}’ = \boldsymbol{z}\). Do we even need uniform crossover?

This table from Differential Evolution – A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces shows the parameters they used on a fairly large test suite of objective functions:

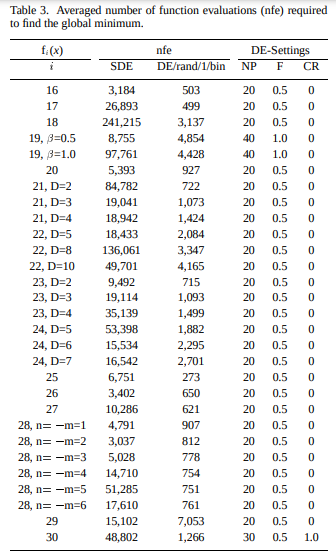
The CR column gives the crossover probability. Its basically always zero! Recall that in official implementations, crossover in Differential Evolution is guaranteed to mutate at least one component.

According to Differential Evolution: A Practical Guide to Global Optimization, this paper somewhat confused the community, because functions tended to either be solved best with \(p \approx 0\) or with \(p \approx 1\). It wasn’t until later that people made the connection that the functions that were solved with \(p \approx 0\) were decomposable, and the functions with \(p \approx 1\) were not.

A function is decomposable if it can be written as a sum of functions using distinct subsets of the inputs, such as:

\[f(\boldsymbol{x}) = \sum_i f^{(i)}(x_i)\]

When this is the case, we can improve individual components in isolation without having to be in-sync with the other components. Small mutation rates are reliable, because we can just reliably adjust a few components at a time and step our way to a minimum. By changing fewer components we have a smaller chance of messing something else up.

Most of the interesting objective functions have a high degree of coupling, and we can’t get away with optimizing some variables in isolation. For example, a neural network mixes its inputs in a convoluted manner. In order to make progress we often have to step in multiple component directions at the same time, which for Differential Evolution requires a higher crossover probability.

Optimizing Decomposable and Non-decomposable Functions

Let’s run another experiment. We’ll again do 1000 trials each (population size 20) with a bunch of versions of Differential Evolution. In the first trial, we’ll optimize a decomposable function, 10 parallel copies of Ackley’s function (making this a 20-dimensional optimization problem):

n_copies = 10
f = x -> sum(100*(x[2i-1]^2-x[2i])^2 + (1-x[2i-1])^2 for i in 1:n_copies)

We’re going to vary the mutation rate. If our results match with the literature, we expect very low mutation rates to do better.

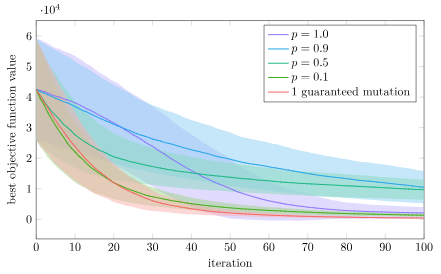
We do indeed find that low mutation rates do better. In fact, a mutation rate of zero with one guaranteed mutation is the best, closely followed by \(p = 0.1\). This does well because taking a small step in just one or two axes can more reliably lead to a win rather than moving in a bunch of axes, and this “knowledge” gained in one individual can easily be copied to other individuals to improve them too.

We can do another experiment with a non-decomposable function, in this case the xor problem. Let’s optimize some basic 2-layer feedforward neural networks. These networks have 21 parameters, so this is a 21-parameter optimization problem:

relu(x) = max(x,0.0)
sigmoid(x) = 1/(1+exp(-x))

function binary_cross_entropy(y_true, y_pred; ϵ=1e-15)
    y_pred = clamp.(y_pred, ϵ, 1-ϵ)
    return -mean(y_true .* log.(y_pred) + (1.-y_true) .* log.(1.-y_pred))
end

# xor problem
f = x -> begin
    inputs = randn(2,10)
    W1 = reshape(x[1:10], (5,2))
    b1 = x[11:15]
    W2 = reshape(x[16:20], (1,5))
    b2 = x[21]
    
    hidden = relu.(W1*inputs .+ b1)
    y_pred = sigmoid.(W2*hidden .+ b2)

    truth_values = inputs .> 0.0
    y_true = .!=(truth_values[1, :], truth_values[2, :])
    
    return binary_cross_entropy(y_true, y_pred)
end

This optimization problem is not decomposable. Taking steps in only one axis at a time is less likely to lead to significant improvements.

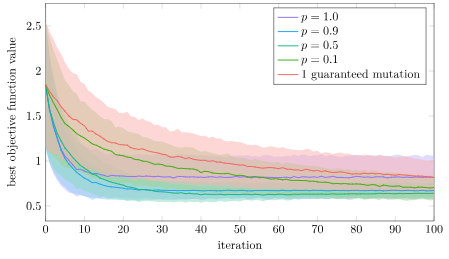
Again, that is what we see! Here the single guaranteed mutation is the worst. Interestingly, full crossover with \(p=1.0\) is initially pretty good but then tapers off, so there does appear to be some advantage to some crossover randomness. The lowest loss is most consistently achieved with \(p=0.5\), but \(p=0.9\) does nearly as well.

Why is full crossover not as good? I suspect that version will more quickly concentrate its populations into local regions, whereas having some stochasticity spreads the populations out more. Let’s plot the mean pairwise distance in the population for this experiment:

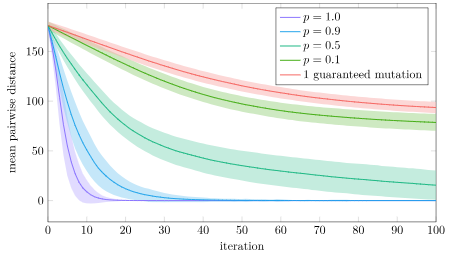
Yup! That’s exactly what we see. With full crossover, our population prematurely converges in about 20 iterations. With \(p=0.9\) it also converges pretty quick, but it apparently has enough time to find a better solution. The other crossover rates are able to avoid that premature convergence.

Conclusion

So now we know a thing or two about what makes Differential Evolution work. To recap, it uses:

  • the differential between two individuals to provide perturbations, which let us explore
  • this differential automatically produces smaller perturbations as the population converges
  • applies the perturbation to a baseline individual which can automatically warp designs to more favorable regions
  • uses uniform crossover to either
    • \(p \approx 0\) force steps in a small set of coordinates; useful for separable functions
    • \(p \geq 0.5\) allow for steps in many coordinates, while preventing premature convergence

So all of the ingredients have their place! Now its time to condense these learnings and add them to the next edition of the textbook.

Cheers.

Optimization is Ax = b

by

One of the most interesting parts of the Convex Optimization lectures by Stephen Boyd was the realization that (continuous) optimization more-or-less boils down to repeatedly solving Ax = b. I found this quite interesting and thought I’d write a little post about it.

Constrained Optimization

An inequality-constrained optimization problem has the form:

\[\begin{aligned}\underset{\boldsymbol{x}}{\text{minimize}} & & f(\boldsymbol{x}) \\ \text{subject to} & & \boldsymbol{g}(\boldsymbol{x}) \leq \boldsymbol{0}\end{aligned}\]

One popular algorithm for solving this problem is the interior point method, which applies a penalty function that prevents iterates \(\boldsymbol{x}^{(k)}\) from becoming infeasible. One common penality function is the log barrier, which transforms our constrained optimization problem into an unconstrained optimization problem:

\[\underset{\boldsymbol{x}}{\text{minimize}} \enspace f(\boldsymbol x) \> – \> \frac{1}{\rho}
\sum_i \begin{cases}
\log\left(-g_i(\boldsymbol x)\right) & \text{if } g_i(\boldsymbol x) \geq -1 \\
0 & \text{otherwise}
\end{cases}\]

or even just

\[\underset{\boldsymbol{x}}{\text{minimize}} \enspace f(\boldsymbol x) \> – \> \frac{1}{\rho}
\sum_i \log\left(-g_i(\boldsymbol x)\right)\]

The penalty scalar \(\rho > 0\) starts small and is increased as we iterate, reducing the penalty for approaching the constraint boundary.

We thus solve our constrained optimization problem by starting with some feasible \(\boldsymbol x^{(0)}\) and then solving a series of unconstrained optimizations. So the first takeaway is that constrained optimization is often solved with iterated unconstrained optimization.

Here we see the an objective function (blue) constrained with \(x \geq 1\) (gray line). The red line shows the penalized surrogate objective. As we increase \(\rho\) and optimize, our solution moves closer and closer to \(x = 1\).

Unconstrained Optimizaton

We have found that constrained optimization can be solved by solving a series of unconstrained optimization problems.

An unconstrained optimization problem has the form:

\[\begin{aligned}\underset{\boldsymbol{x}}{\text{minimize}} & & f(\boldsymbol{x}) \end{aligned} \]

If \(f\) is continuous and twice-differentiable, we can solve this problem with Newton’s method. Here we fit a quadratic function using the local gradient and curvature and use its minimum (which we can solve for exactly) as the next iterate:

\[\boldsymbol x^{(k+1)} = \boldsymbol x^{(k)} \> – \> \boldsymbol H(\boldsymbol x^{(k)})^{-1} \nabla f(x^{(k)})\]

Continuous functions tend to become bowl-shaped close to their optimas, so Newton’s method tends to converge extremely quickly once we get close. Here is how that looks on the banana function:

What this means is that unconstrained optimization is done by repeatedly calculating Newton steps. Calculating \(\boldsymbol H(\boldsymbol x^{(k)})^{-1} \nabla f(x^{(k)})\) is the same as solving Ax = b:

\[\boldsymbol H\boldsymbol d = \nabla f\]

Well alrighty then, optimization is indeed a bunch of Ax = b.

What does this Mean

There are several takeaways.

One is that its nice that complicated things are just made up of simpler things that we can understand. One can take comfort in knowing that the world is understandable.

Another is that we should pay a lot of attention to how we compute Ax = b. Most of our time spent optimizing is spent solving Ax = b. If we can do that more efficiently, then we can optimize a whole lot faster.

Estimating Solve Times

How long does it take to solve Ax = b? Well, that depends. Let’s say we’re naive, and we have a random \(n \times n\) matrix \(\boldsymbol A\) and a random vector \(\boldsymbol b\). How fast can our computers solve that?

Well, it turns out that my laptop can solve a random \(1000 \times 1000\) linear system in about 0.35s:

We can plot the computation time vs. matrix size:

At first glance, what we see is that yes, computation grows as we increase \(n\). Things get a little fishy though. That trend line is \(n^2/10^7\), which is not the \(O(n^2)\) growth that we expected. What is going on?

While Julia itself is running single-threaded, the underlying BLAS library can use up to 8 threads:

Our system is sneakily making things more efficient! If we force BLAS to be single-threaded, we get the \(O(n^3)\) growth we expected after about \(n=200\) (Thank you Julia Discourse!):

What we’ve learned is pretty important – there are speedups to be had that go beyond traditional big-O notation. If you have an optimization problem, chances are that multithreading and SIMD can speed things up for you. If you have a really large optimization problem, maybe you can distribute it across multiple machines (Proximal methods, for example, are often amenable to this).

We also learned how mind-bogglingly fast linear algebra is, even on a single thread. Think about how long it would take you to manually solve Ax = b for \(n=2\) with pen and paper, and how fast the same operation would take on your machine.

If it takes 100 Newton iterates to solve an unconstrained optimization problem, then you can solve a problem with a thousand variables in 3.5s. Multiply that by another 100 for a constrained optimization problem, and you’re looking at solving a constrained optimization problem with \(n=1000\) in under 6 minutes (and often in practice, much faster).

We live in an era where we can solve extremely large problems (GPT-4 is estimated to have 1.7 billion parameters), but we can also solve smaller problems really quickly. As engineers and designers, we should feel empowered to leverage these capabilities to improve everything.

Special Structure

Appendix C of Convex Optimization talks a lot about how to solve Ax = b. For starters, generally solving \(\boldsymbol A \boldsymbol x = \boldsymbol b\) for an arbitrary \(\boldsymbol A \in \mathbb{R}^n\) and \(\boldsymbol b \in \mathbb{R}^n\) is \(O(n^3)\). When we’re using Newton’s method, we know that the Hessian is symmetric and positive definite, so we can compute the Cholesky decomposition of \(\boldsymbol A = \boldsymbol F^\top \boldsymbol F\). Overall, this takes about half as many flops as Gaussian elimination [source].

There are a bunch of other types of structure that we can take advantage of when we know that it exists. The most obvious is when \(\boldsymbol A\) is diagonal, in which case solving Ax = b is \(O(n)\).

One particularly interesting example is when \(\boldsymbol A\) has arrow structure:

When this happens, we have to solve:

\[\begin{bmatrix} \boldsymbol A & \boldsymbol B \\ \boldsymbol B^\top & \boldsymbol C \end{bmatrix} \begin{bmatrix} \boldsymbol x \\ \boldsymbol y \end{bmatrix} = \begin{bmatrix}\boldsymbol b \\ \boldsymbol c\end{bmatrix}\]
where \( \boldsymbol A\) is diagonal, block-diagonal, or banded; \(\boldsymbol B\) is long and narrow; and \(\boldsymbol C\) is dense but comparatively small.

Solving a system with arrow structure can be done by first solving \(\boldsymbol A \boldsymbol u = \boldsymbol b\) and \(\boldsymbol A \boldsymbol V = \boldsymbol B\), which are both fast because we can exploit \( \boldsymbol A\)’s structure. Expanding the top row and solving gives us:

\[\boldsymbol x = \boldsymbol A^{-1} \left( \boldsymbol b – \boldsymbol B \boldsymbol y \right) = \boldsymbol u \> – \boldsymbol V \boldsymbol y\]

We can substitute this into the bottom row to get:

\[\begin{aligned} \boldsymbol B^\top \boldsymbol x + \boldsymbol C \boldsymbol y & = \boldsymbol c \\ \boldsymbol B^\top \left( \boldsymbol u \> – \boldsymbol V \boldsymbol y \right) + \boldsymbol C \boldsymbol y & = \boldsymbol c \\ \left( \boldsymbol C – \boldsymbol B^\top \boldsymbol V\right) \boldsymbol y & = \boldsymbol c \> – \boldsymbol B^\top \boldsymbol u\end{aligned}\]

Having solved that dense system of equations for \(\boldsymbol y\), we can back out \(\boldsymbol x\) from the first equation and we’re done.

You might think that arrow structure is a niche nicety that never actually happens. Well, if you look at how packages like Convex.jl, cvx, and cvxpy solve convex optimization problems, you’ll find that they expand and transform their input problems into a partitioned canonical form:

\[\begin{aligned}\underset{\boldsymbol x^{(1)}, \ldots, \boldsymbol x^{(k)}}{\text{minimize}} & & d + \sum_{i=1}^k \left(c^{(i)}\right)^\top \boldsymbol x^{(i)} \\ \text{subject to} & & \boldsymbol x^{(i)} \in \mathcal{S}^{(i)} \enspace \text{for } i \text{ in } \{1, \ldots, k\}\\ & & \sum_{i=1}^k \boldsymbol A^{(i)} \boldsymbol x^{(i)} = \boldsymbol b\end{aligned}\]

If we apply an interior point method to this:

\[\begin{aligned}\underset{\boldsymbol x}{\text{minimize}} & & d + \boldsymbol c^\top \boldsymbol x + \frac{1}{\rho} p_\text{barrier}(\boldsymbol x) \\ \text{subject to} & & \boldsymbol A^\top \boldsymbol x = \boldsymbol b\end{aligned}\]

we can apply a primal-dual version of Newton’s method that finds a search direction for both \(\boldsymbol x\) and the dual variables \(\boldsymbol \mu\) by solving:

\[\begin{bmatrix} \nabla^2 p_\text{barrier}(\boldsymbol x) & \boldsymbol A^\top \\ \boldsymbol A & \boldsymbol 0\end{bmatrix} \begin{bmatrix}\Delta \boldsymbol x \\ \boldsymbol \mu \end{bmatrix} = – \begin{bmatrix}\rho \boldsymbol c + \nabla p_\text{barrier}(\boldsymbol x) \\ \boldsymbol A \boldsymbol x – \boldsymbol b\end{bmatrix}\]

Wait, what is that we see here? Not only does this have arrow structure (The Hessian matrix \(\nabla^2 p_\text{barrier}(\boldsymbol x)\) is block-diagonal), but the tip of the arrow is zero! We can thus solve for the Newton step very efficiently, even for very large \(n\).

So this esoteric arrow-structure thing turns out to be applicable to general convex optimization.

Conclusion

If you take a look at university course listings, there is a clear pattern of having classes for “Linear X” and “Nonlinear X”. For example, “EE263: Introduction to Linear Dynamical Systems” and “E209B Advanced Nonlinear Control”. You learn the linear version first. Why? Because we’re really good at solving linear problems, so whenever a problem can be framed or approximated in a linear sense, we’ve either solved it that way first or found its easiest to teach it that way first. Anything can be locally approximated by a 1st-order Taylor series and we can just work with a linear system of equations.

I love that insight, but I also love the implication that it has. If we can understand how to work with linear systems, how to exploit their structure and how to solve them quickly to sufficient accuracy, then we can speed up the solution of pretty much any problem we care about. That means we can solve pretty much any problem we care about better, more often, to a higher-degree of precision, and thereby make the world a better place.