I recently happened upon a video on YouTube in which JDH implements a Doom clone. He does this in C, without any graphics libraries. Just SDL and a pixel buffer:

u32 pixels[SCREEN_SIZE_X * SCREEN_SIZE_Y]; 

The video blew me away. I have long admired how John Carmack et. al. were the first to create playable fast-paced 3D games. It was a technical achievement and a true breakthrough. There is also something clean and pure about restricting oneself to pure C. It is closer to the hardware. You’re setting each pixel byte by byte. You’re totally in control.

I had another project in the works, but this video just kept turning over in my head. I decided to give the first part, rendering for Wolfenstein 3D in pure C, a stab myselfclarificationBy this I mean deriving and implementing the rendering, and figuring out how to get a C environment set up locally. I heavily leaned on JDH's video to help me get started with the base code structure..

This post is my attempt at doing Wolfenstein-style rendering, based on gameplay I saw at the beginning of JDH’s video. It is probably not exactly what happens in Wolfenstein, but I’m hoping its somewhat close. I plan to check back with a future post to see where / how things diverge.

Setup

The biggest hurdle to getting started was setting myself up to program in C. I have no pure-C projects. Heck, even pure C++ projects can be a pain to set up.

I typically program in Sublime Text and compile in the terminal. However, for this I wanted to use Visual Studio Code. It seems to have the best debugger integration, and I feel like all game-programming folks that I follow use it. I have not used VS code on personal projects, so I figured this would be a great opportunity to change that.

As per usual, getting this all to work requiring some Googling and messing around for a while. I figure it’s worth talking about the process, at the very least so that I can refer to it myself in the future when I set up new projects. I’ll cover that at the end of this post, but for now let’s jump straight to C programming.

SDL Game Loop

We have to get a window we can render to and establish a basic game loop. This has the form:

int main(int argc, char *argv[]) {
   ... init things like the window ...
   
   // main loop
   while (state.quit == 0) {
      ProcessEvents();
      TickGame(dt);
      RenderToPixelBuffer();
      PresentPixelBuffer();
   }
}

One iteration through the main loop corresponds to one frame of our game. If the game runs at 30Hz, then we looping through this 30 times per second.

• ProcessEvents – Games and other programs need to react to player inputs. Rather than have callbacks that interrupt your game in the middle of what its doing, SDL collects everything that happens in an event queue. We start every frame by emptying the queue and processing all of the events to determine how they impact our game.
  For example, if the player hits the ‘w’ key, we might want to store that information to later use it to move the player forward.
• TickGame – This method updates the game state. In a larger game this would do a whole lot more work. Here we’re basically just updating the player’s position, orientation, and velocity based on keyboard inputs.
• RenderToPixelBuffer – This is the core part of what makes this project exciting. Here we render the world state by setting color values in our pixel buffer. We have to render based on the camera’s current location and orientation, and use that information to get the pixels right.
• PresentPixelBuffer – Here we ask SDL to take our pixels and show them on the screen. In my case, this presentation code has vsync enabled, so it is sychronized with the monitor refresh rate. This automatically waits the appropriate amount of time to update at that rate. In my case, that means the program ends up executing at 30Hz, despite being able to technically run much faster.

As far as SDL goes, we have to initialize a window, a texture, and a renderer. The window controls the actual window panel that shows up on our screen. The texture associated with the window contains the pixel data that is presented in the window. The renderer is needed for transferring our pixel buffer to the texture.

We copy our pixel buffer into this texture at the end of every frame. JDH created his texture with the pixel format SDL_PIXELFORMAT_ABGR8888, which means that every byte is an unsigned 32-bit number with 1 byte each for alpha, blue, green, and red. Thus, 0xFF00FF00 is opaque green.

We additionally maintain a pixel buffer:

u32 pixels[SCREEN_SIZE_X * SCREEN_SIZE_Y];

This pixel buffer is what we will manipulate in order to depict the 3D world “seen” by our player camera. Each pixel is also a 32-bit ABGR value.

For example, the following produces:

int x = 52;
int y = 75;
state.pixels[(y * SCREEN_SIZE_X) + x] = 0xFFFF00FF;

We’ve got a lot of pixel work ahead of us to go from this to 3D graphics. But therein lies the challenge! No rendering libraries, just algorithms and math 😀

Problem

A Wolfenstein level is defined on a 2D grid. Grid tiles can be solid or empty, with walls taking up exactly one grid tile. Our camera only ever rotates horizontally, never vertically. These facts make rendering 3D scenes so much easier than general 3D rendering.

The grid dimensions are defined by two numbers – the tile width and the wall height:

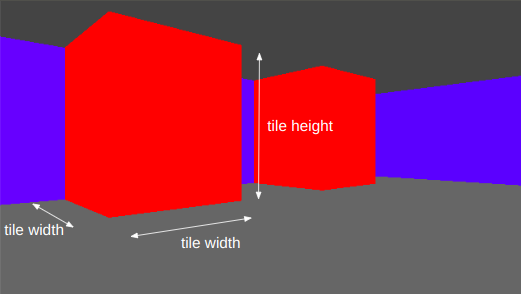
In this case I’m using 1.0 and 1.2 units of length, respectively.

Our player exists at some 2D location within this world, and is facing in some direction. Our camera is coincident with the player and faces the same direction:

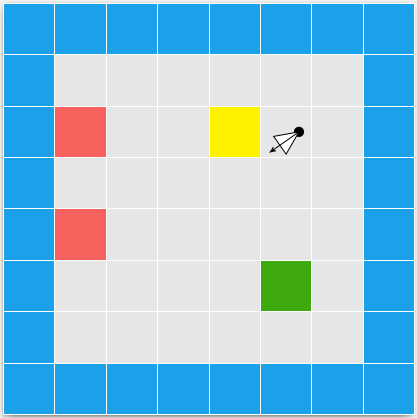
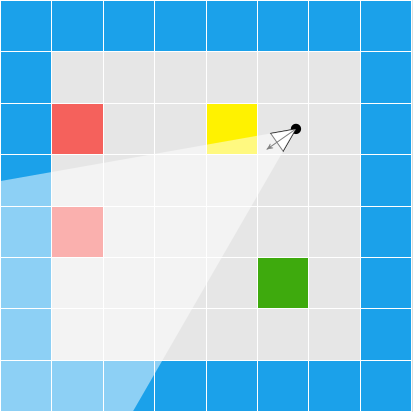
The camera has a horizontal and vertical field of view. In the top-down 2D perspective we can see its horizontal field of view:

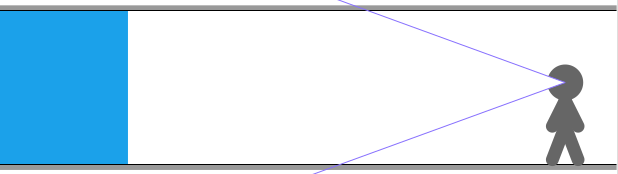
In a side 2D perspective we can see its vertical field of view:

We can imagine our game screen being a plane lying in this field of view, fairly close to the player. Our objective is to set each pixel based on what the camera “sees” at that pixel’s location. The color is determined by the object we intersect with if we cast a ray from the camera’s origin, through the pixel, and then intersect with the world:

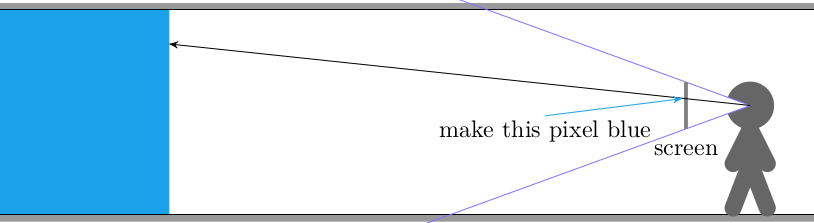
In the case of a 2D cross-section, a bottom stretch of pixels are colored the floor’s color, a top stretch of pixels are colored the ceiling’s color, and everything in between is colored the block’s color:

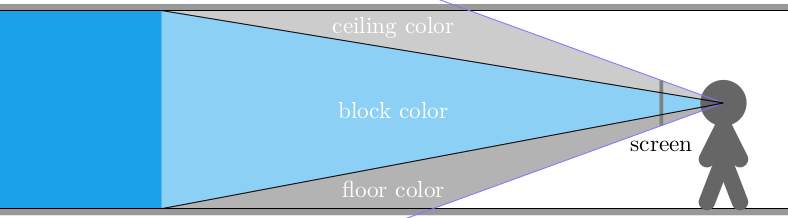
Wolfenstein’s blocky world and consistent floor and ceiling height mean we can get all the information we need to render a column of pixels by doing a single horizontal ray cast:

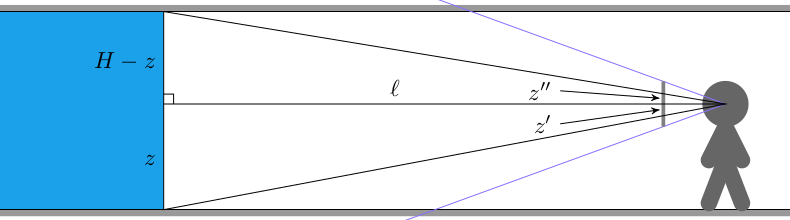
We can use the fact that the larger triangles formed with the full raycast distance are similar to the triangles that from the camera plane a distance \(d=1\) from the player. If the raycast distance is \(\ell\), the player’s height is \(z\), and the wall height is \(H\), then:

\[z’ = \frac{d z}{\ell}, \qquad z” = \frac{d(H-z)}{\ell}\]

If we have \(n\) pixels per column (in my case, 360), then we need to fill pixels according to:

\[\begin{cases} \text{floor color} & \text{if } y < n/2 – \frac{d z}{\ell} n \\ \text{wall color} & \text{if } y < n/2 + \frac{d(H-z)}{\ell} n \\ \text{ceiling color} & \text{otherwise} \end{cases}\]

// Calculate the pixel bounds that we fill the wall in for
int y_lo = (int)(SCREEN_SIZE_Y/2.0f - cam_len*state.camera_z/ray_len * SCREEN_SIZE_Y / state.camera_height);
int y_hi = (int)(SCREEN_SIZE_Y/2.0f + cam_len*(WALL_HEIGHT - state.camera_z)/ray_len * SCREEN_SIZE_Y / state.camera_height);
y_lo = max(y_lo, 0);
y_hi = min(y_hi, SCREEN_SIZE_Y-1);

fill_column(x, 0, y_lo-1, color_floor);
fill_column(x, y_lo, y_hi, color_wall);
fill_column(x, y_hi + 1, SCREEN_SIZE_Y-1, color_ceil);

Next we have to figure out how to do the ray cast to get \(\ell\). We need to perform a ray cast for every column of pixels on our screen. Each such ray will originate at the player’s location, and then head in the direction of its pixel column until it strikes a wall. The distance traveled is \(\ell\). For example:

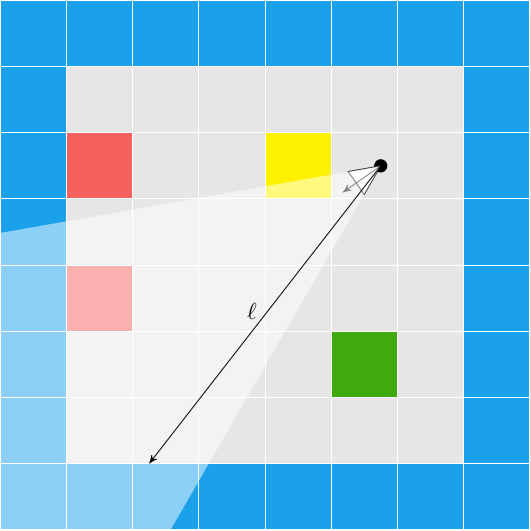
We can leverage the fact that we have a grid. We know that the intersection point, when we eventually find it, will lie on one of the grid’s horizontal or vertical lines.

Let’s start by decomposing our initial coordinate, the camera position \((p_x, p_y)\), into its tile indices and offsets from the tile’s bottom-left corner:

int x_ind_cam = (int)(floorf(state.camera_pos.x / TILE_WIDTH));
int y_ind_cam = (int)(floorf(state.camera_pos.y / TILE_WIDTH));
f32 x_rem_cam = state.camera_pos.x - TILE_WIDTH*x_ind_cam;
f32 y_rem_cam = state.camera_pos.y - TILE_WIDTH*y_ind_cam;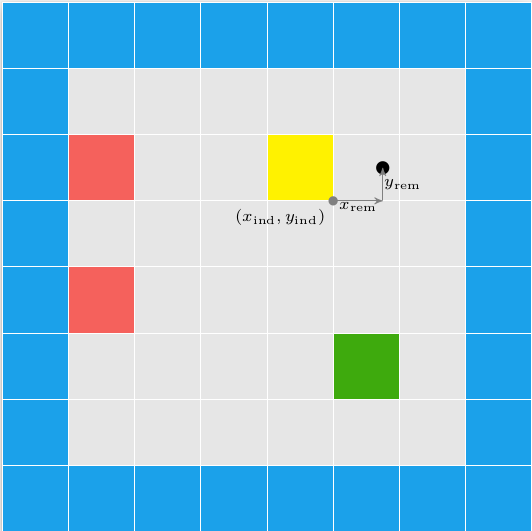

The raycast direction can be calculated from the pixel column position. We assume the camera screen is a unit distance \(d = 1\) from the camera, \(\boldsymbol{c}\). The raycast direction is a function of the camera’s width \(w\), the number of screen pixels \(m\), and the direction the camera is facing, \(\hat{\boldsymbol{b}}\):

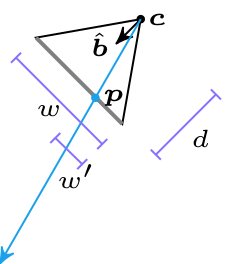
We can locate the pixel’s location \(\boldsymbol{p}\) as:

\[\boldsymbol{p} = \boldsymbol{c} + d \hat{\boldsymbol{b}} + \left(\frac{w}{2} – w \frac{x}{m}\right) \texttt{rotr}(\hat{\boldsymbol{b}}) = \boldsymbol{c} + d \hat{\boldsymbol{b}} + \left(\frac{w}{2} – w’\right) \texttt{rotr}(\hat{\boldsymbol{b}})\]

Here \(\texttt{rotr}(\hat{\boldsymbol{b}})\) is the camera direction rotated by 90 degrees in the right-hand direction (counter clockwise).

The raycast direction is aligned with \(\bar{\boldsymbol{pc}}\):

\[\bar{\boldsymbol{pc}} = \boldsymbol{p} – \boldsymbol{c} = \boldsymbol{c} + d \hat{\boldsymbol{b}} + \left(\frac{w}{2} – w \frac{x}{m}\right) \texttt{rotr}(\hat{\boldsymbol{b}})\]

We can normalize \(\bar{\boldsymbol{pc}}\) by dividing by its length to produce our raycast direction \(\hat{\boldsymbol{r}}\).

Raycasting

Now that we have our ray origin and unit direction, we can cast it out into the map. If we imagine that the ray is travelling at unit speed, then its position vs. time within its current cell is:

\[\begin{aligned} x(t) & = x_\text{rem} + \hat{r}_x dt \\ y(t) & = y_\text{rem} + \hat{r}_y dt \end{aligned} \]

The direction the ray is facing determines when it will cross certain tile boundaries:

• We cross \(x_\text{rem} = 0\) if \(\hat{r}_x <0\), at \(dt = -x_\text{rem} / \hat{r}_x\)
• We cross \(x_\text{rem} = w_\text{TILE}\) if \(\hat{r}_x > 0\), at \(dt = (w_\text{TILE} – x_\text{rem}) / \hat{r}_x\)
• We cross \(y_\text{rem} = 0\) if \(\hat{r}_y <0\), at \(dt = -y_\text{rem} / \hat{r}_y\)
• We cross \(y_\text{rem} = w_\text{TILE}\) if \(\hat{r}_y > 0\), at \(dt = (w_\text{TILE} – y_\text{rem}) / \hat{r}_y\)

We can generalize this to avoid having a bunch of if statements in our code:

• if \(\hat{r}_x < 0\), then \(dt = -1/\hat{r}_x \cdot x_\text{rem} + 0\) and \(x_\text{ind}\) will decrease by 1
• if \(\hat{r}_x > 0\), then \(dt = -1/\hat{r}_x \cdot x_\text{rem} + w_\text{TILE}/\hat{r}_x\) and \(x_\text{ind}\) will increase by 1
• if \(\hat{r}_x = 0\), then \(dt = 0 \cdot x_\text{rem} + \infty\) and \(x_\text{ind}\) will not change

We can use the same statements for the y direction.

This simplifies walking across the grid to calculating \(dt\) for x and y, and selecting whichever one is smaller (the earlier crossing). We then update our decomposed position (tile index and remaining offset) appropriately. This process continues until we enter a solid tile.

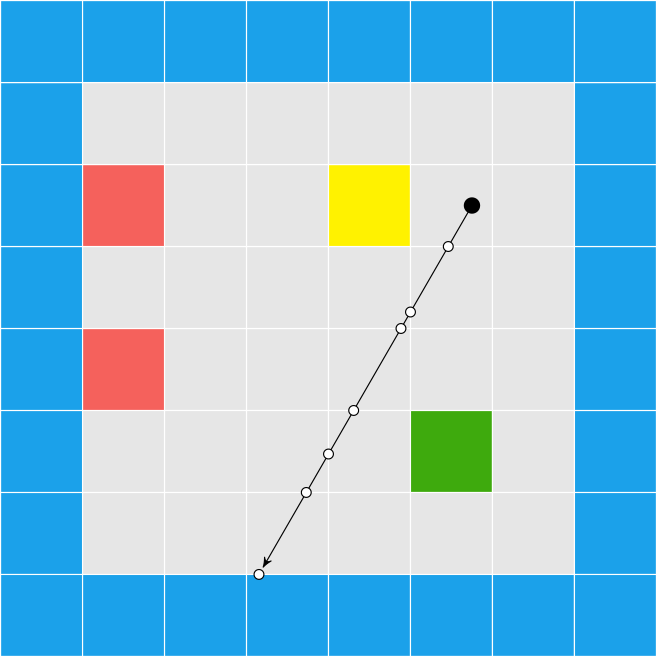
while (true) {
   f32 dt_best = INFINITY;
   dx_ind = 0;
   dy_ind = 0;
            
   f32 dt_x = dx_a*x_rem + dx_b;
   f32 dt_y = dy_a*y_rem + dy_b;
   if (dt_x < dt_y) {
       dt_best = dt_x;
       dx_ind = dx_ind_dir;
       dy_ind = 0;
   } else {
       dt_best = dt_y;
       dx_ind = 0;
       dy_ind = dy_ind_dir;
   }

   // Move up to the next cell
   x_ind += dx_ind;
   y_ind += dy_ind;
   x_rem += dir.x * dt_best - TILE_WIDTH*dx_ind;
   y_rem += dir.y * dt_best - TILE_WIDTH*dy_ind;

   // Check to see if the new cell is solid
   if (MAPDATA[y_ind*8 + x_ind] > 0) {
      break;
   }
}

Once we’ve collided, we can back out the raycast length. We know from the tile and from which direction we entered it what color we should render it, if we have different colors for different blocks. We can even employ a basic lighting trick where we color x-sides differently than y-sides:

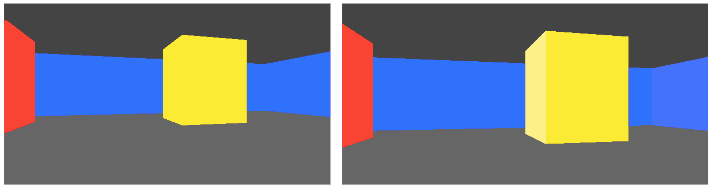
And that’s it! We’ve got basic 3d graphics on the screen.

Profiling

I was curious how efficient this code is, and tried to measure it. I initially used SDL_GetTicks to measure the framerate in milliseconds, only to discover that SDL_RenderPresent is automatically vsyncing with the display to 30 Hz. So I wrapped everything before the SDL calls between sys/time.h gettimeofday calls. I am currently getting about 4.5ms per frame, which is 222 frames per second.

I’m certainly happy with that. I’m sure there are plenty of additional tricks that could be employed, and if things grow in complexity that headroom could very quickly be eaten away. I am planning on looking into how Wolfenstein rendering is _actually_ done.

Conclusion

Rendering in general 3D spaces with arbitrary object geometry and orientations is pretty tricky. Rendering when you constrain yourself to a grid world where you can only look horizontally is a lot easier. Granted, this demo only scratched the basics, but its still pretty cool to see how quickly one can get something neat up and running with some math and code.

The code for this demo is available here.

Special thanks to JDH for the inspiration to pursue this and for the reference code to get up and running.

Getting Started with VS Code on Ubuntu

In this section I wanted to give some pointers on how to set oneself up with Visual Studio Code on Ubuntu.

To start, I downloaded VS Code. For Ubuntu, that means downloading the .deb file. I then installed it with:

sudo apt install ./<file>.deb

I then installed SDL2:

sudo apt install libsdl2-dev libsdl2-2.0-0

I then installed some recommended VS code extensions. To do that, you have to navigate via the left-hand bar to the tetris-like icon:

Then, use the provided search bar to find C/C++:

You can click on that extension and install it.

I similarly installed:

• C/C++ Makefile Project by Adriano Markovic
• C/C++ Runner by franneck94
• Code Runner by Jun Han
• CodeLLDB by Vadim Chugunov

Each VS Code project is contained inside a workspace. I created a new folder on my machine and navigated to it inside the VS code terminal. I then initialized a new project with Ctrl + Shift + P, and selected “C/C++ Make: INIT Project”. This creates a new C/C++ project with a Makefile.

I then edited the Makefile to link to SDL2 and math.h:

CXXFLAGS = -std=c11 -Wall -g # Note: -g adds proper debugging with symbols
LDFLAGS = -lSDL2 -lm

and named my program:

APPNAME = TOOM

I created a new directory, src, and created a new file, main.c inside of it. That’s where the coding starts!

#include <math.h>
#include <stdio.h>
#include <SDL2/SDL.h>
int main(int argc, char *argv[]) {
    printf("Hello World!\n");
    return 0;
}

At this point I could make the project in the terminal by typing make, and could execute it by typing ./TOOM. However, to use the debugger, I needed to set up a tasks.json file in the generated .vscode directory:

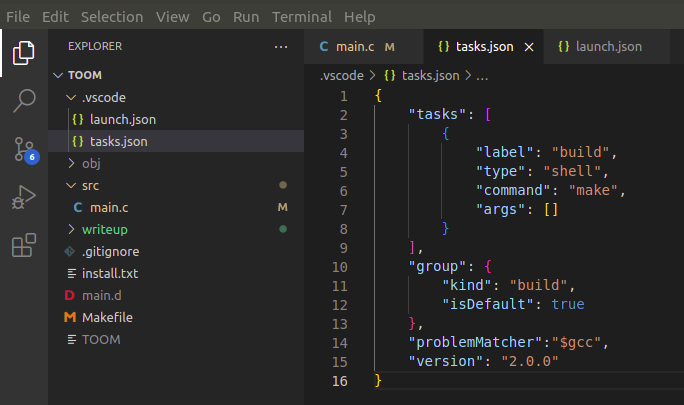
Then, opening the debugger via the left-column icon and hitting the settings gear icon creates a launch.json file. I set this to run the prelaunch task “build” which we just set up in tasks.json. The overall config looks like this:

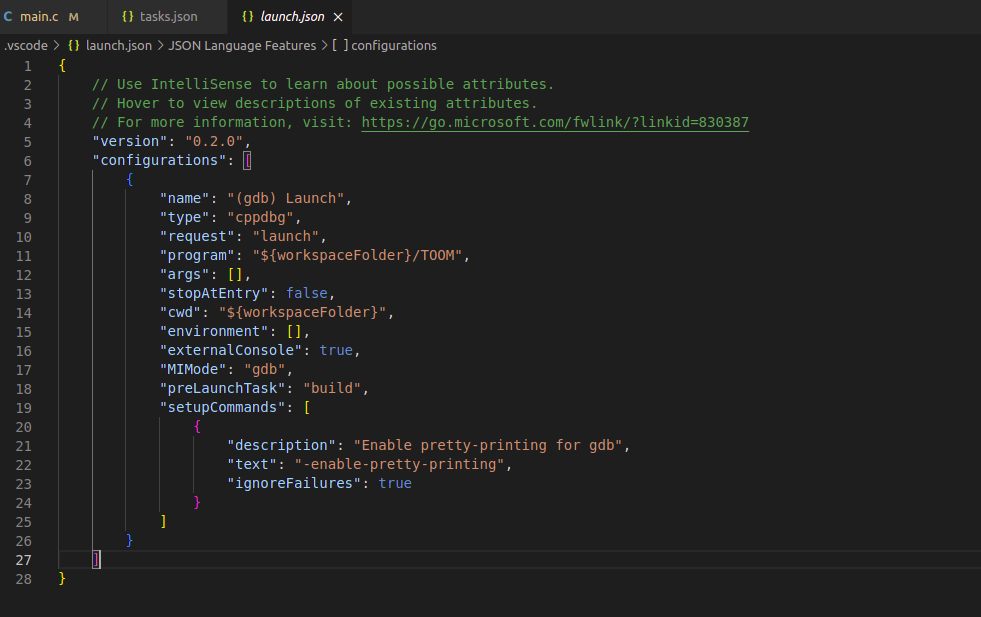
This lets you set breakpoints in your code and execute in debug mode. You can use VS code’s fantastic introspection tools to see variable values and see what your program is up to.