My last few blog posts covered methods for getting push-optimal solutions to simple Sokoban puzzles. Traditional Sokoban, however, operates on player moves. Solvers often reason about pushes to simplify decision-making. Unfortunately, push-optimal solutions are not necessarily move-optimal. For example, this solution is push-optimal but has some very clear inefficiencies when we render out the player moves required to travel between boxes:

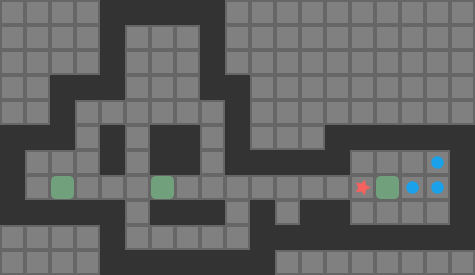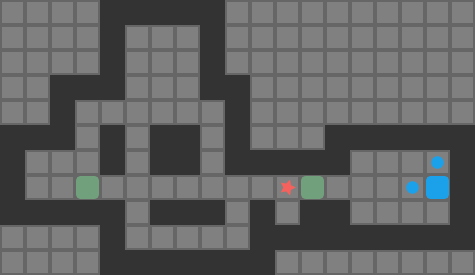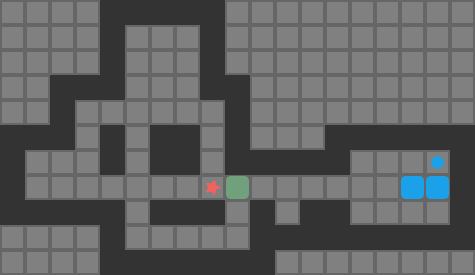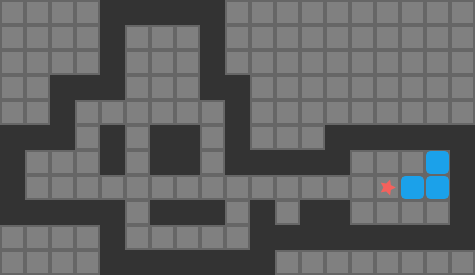
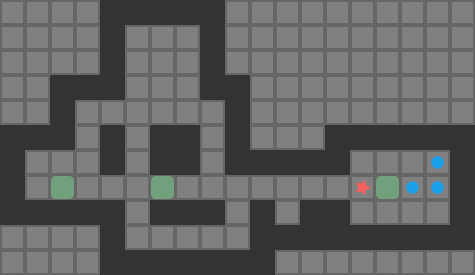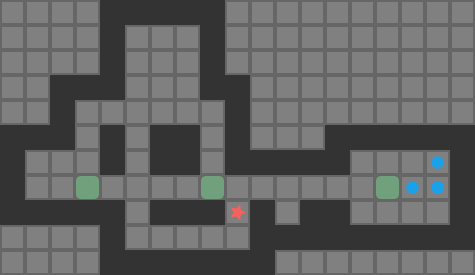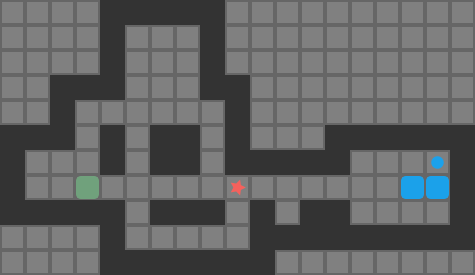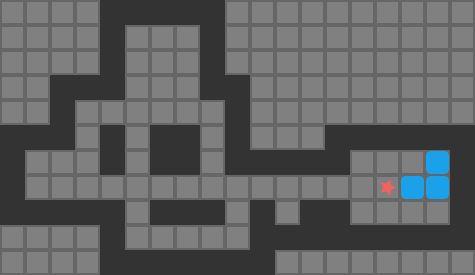
Directly solving for move-optimal solutions from scratch is difficult. Rather than doing that, it is common to optimize a given solution to try to find another solution with a smaller player move count. Thus, Sokoban solvers typically find push-optimal solutions, or more commonly some valid solution, and Sokoban optimizers work with an existing solution to try and improve it.

There are many approaches for optimizing solutions. In this post, I’ll just cover some very basic approaches to improve my push-optimal solutions from the previous posts.

Solution Evaluation

Every optimization problem needs an objective function. Here, we are trying to find solutions with fewer player moves. As such, our objective function takes in a potential push sequence solution and evaluates both its validity (whether it is, in fact, a solution), and the number of player moves. The number of player moves is the number of box pushes plus the number of moves to walk to the appropriate location for each push.

All of the strategies I use here simply shuffle the pushes around. I do not change the pushes. As we’ll see, this basic assumption works pretty well for the problems at hand.

We thus have a simple constrained optimization problem – to minimize the number of player moves by permuting the pushes in a provided push-optimal solution subject to the constraint that we maintain solution integrity. We can easily evaluate a given push sequence for validity by playing the game through with that push sequence, which we have to do anyway to calculate the number of player moves.

Strategy 1: Consider all Neighboring Box Pairs

The simplest optimization strategy is to try permuting neighboring push pairs. We consider neighboring pairs because they are temporally close, and thus more likely to be a valid switch. Two pushes that are spread out a lot in time are likely to not be switchable – other pushes are more likely to have to happen in-between.

This strategy is extremely simple. Just iterate over all pushes, and if two neighboring pushes are for two different boxes, try swapping the push order and then evaluating the new push sequence to see if it solves the problem with a smaller move count. If it does, keep the new solution.

For example, if our push sequence, in terms of box pushes, is AAABBCCBAD, we would evaluate AABABCCBAD first, and it does not lead to an improvement, consider AAABCBCBAD next, etc.

Strategy 2: Consider all Neighboring Same-Box Sequences

The strategy above is decent for fine-tuning the final solution. However, by itself it is often unable to make big improvements.

Move-optimal solutions are often achieved by grouping pushes for the same box together. This intuitively leads to the player not having to trek to other boxes between pushes – they are already right next to the box they need to push next. We thus can do quite well by considering moving chunks of pushes for the same box around rather than moving around a single box push at a time.

This approach scans through our pushes, and every time we change which box we are pushing, considers moving forward all push sequences of all other next boxes to before the current sequence of box pushes. For example, if our push sequence is AAABBCCBAD, we would consider BBAAACCBAD, CCAAABBBAD, and DAAABBCCBA, greedily keeping the first one that improves our objective.

Strategy 3: Group Same-Box Push Sequences

The third basic strategy that I implemented moves box sub-sequences in addition to full box sequences in an effort to consolidate same-box push sequences. For each push, if the next push is not for the same box, we find the next push sequence for this box and try to move the largest possible sub-sequence for that box to immediately after our current push – i.e., chaining pushes.

For example, if our push sequence is AAABBCCBAD, we would consider AAAABBCCBD, and if that did not lead to an improvement, would consider AAABBBCCAD.

Similarly, if our push sequence is AAABBAAA, we would consider AAAAAABB, then AAAAABBA, and finally AAAABBAA in an effort to find the largest sub-sequence we could consolidate.

Putting it All Together

None of these heuristics are particularly sophisticated or fancy. However, together we get some nice improvements. We can see the improvement on the full Sokoban 01 problem:

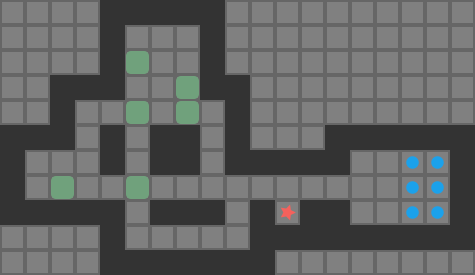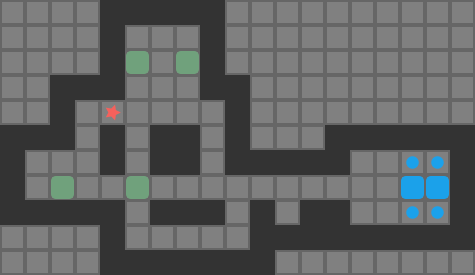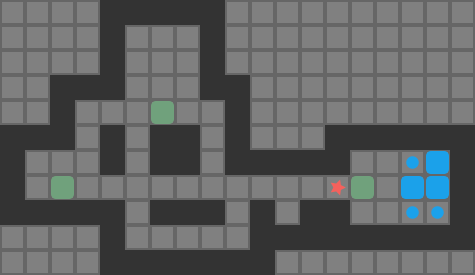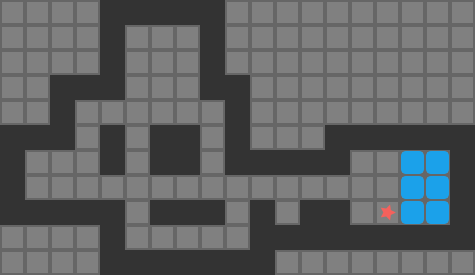
The following output shows how the algorithm progressed:

iteration, push count, number of applications of strategy 1, ... strategy 2, ... strategy 3:
1: 636  0  0  0
dbcffffffffccfffcddccadfcccddbcbaaccdccadddbaddadedaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
2: 598  4  0  1
dbcfffffffffffcccddccadfcccddcbbaacdcccadddbadadeddaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
3: 520  7  0  2
dbcffffffffffffcccddccadcccddcbbaadccccadddbdaaedddaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
4: 504  8  0  3
dbcffffffffffffcccccddadcccddcbbaadccccaddbddaaedddaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
5: 482  8  0  4
dbcffffffffffffccccccccddadddcbbaadccccaddbddaaedddaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
6: 470  8  0  5
dbcffffffffffffcccccccccddadddbbaadccccaddbddaaedddaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
7: 450  8  0  6
dbcffffffffffffcccccccccccccddadddbbaadaddbddaaedddaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
8: 428  9  0  7
dbcffffffffffffcccccccccccccdddddabbaaadddbddaaedddaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
9: 428  9  0  8
dbcffffffffffffcccccccccccccdddddaabbaadddbddaaedddaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
10: 420  9  0  9
dbcffffffffffffcccccccccccccdddddaabbaadddddbaaedddaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
11: 404  9  0  10
dbcffffffffffffcccccccccccccdddddaabbaaddddddddbaaeaaddaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
12: 376  9  0  11
dbcffffffffffffcccccccccccccdddddaabbaaddddddddddbaaeaaaaaebaaaabbddaaeeeeebbeeeebbeeebbbbbbbeebb
13: 376  9  0  12
dbcffffffffffffcccccccccccccdddddaabbaaddddddddddddbaaeaaaaaebaaaabbaaeeeeebbeeeebbeeebbbbbbbeebb
14: 358  9  0  13
dbcffffffffffffcccccccccccccdddddaabbaaddddddddddddbaaaaaaaeebaaaabbaaeeeeebbeeeebbeeebbbbbbbeebb
15: 344  9  0  14
dbcffffffffffffcccccccccccccdddddaabbaaddddddddddddbaaaaaaaaaaaeebbbaaeeeeebbeeeebbeeebbbbbbbeebb
16: 320  9  0  15
dbcffffffffffffcccccccccccccdddddaabbaaddddddddddddbaaaaaaaaaaaaaeebbbeeeeebbeeeebbeeebbbbbbbeebb
17: 302  9  0  16
dbcffffffffffffcccccccccccccdddddaabbaaddddddddddddbaaaaaaaaaaaaaeeeeeeebbbbbeeeebbeeebbbbbbbeebb
18: 286  9  0  17
dbcffffffffffffcccccccccccccdddddaabbaaddddddddddddbaaaaaaaaaaaaaeeeeeeeeeeebbbbbbbeeebbbbbbbeebb
19: 260  9  0  18
dbcffffffffffffcccccccccccccdddddaabbaaddddddddddddbaaaaaaaaaaaaaeeeeeeeeeeeeeebbbbbbbbbbbbbbeebb
20: 260  9  0  19
dbcffffffffffffcccccccccccccdddddaabbaaddddddddddddbaaaaaaaaaaaaaeeeeeeeeeeeeeeeebbbbbbbbbbbbbbbb

So there you have a quick-and-dirty way to get some nicer solutions out of our push-optimal solutions. Other approaches will of course be needed once we have solutions that aren’t push-optimal, which we’ll get once we move onto problems that are too difficult to solve optimally. There we’ll have to do more than just permute the pushes around, but actually try changing our push sequence and refining our solution more generally.

For those interested, the Sokoban Optimizer “Scribbles” by Brian Damgaard are an excellent resource.