Last month I wrote about moving the Sokoban policy training code from CPU to GPU, yielding That significantly shortened both training time and the time it takes to compute basic validation metrics. It has not, unfortunately, significantly changed how long it takes to run rollouts, and relatedly, how long it takes to run beam search.
The Bottleneck
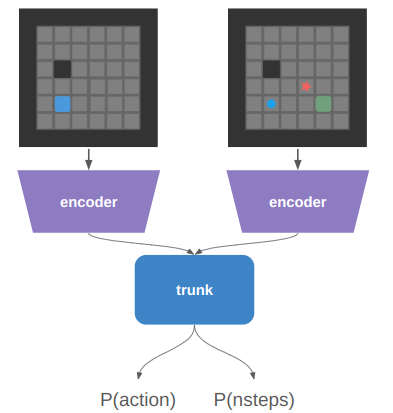
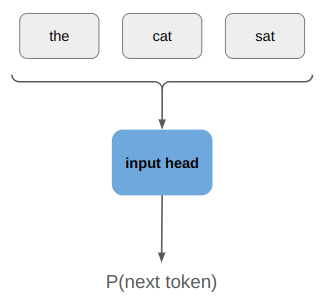
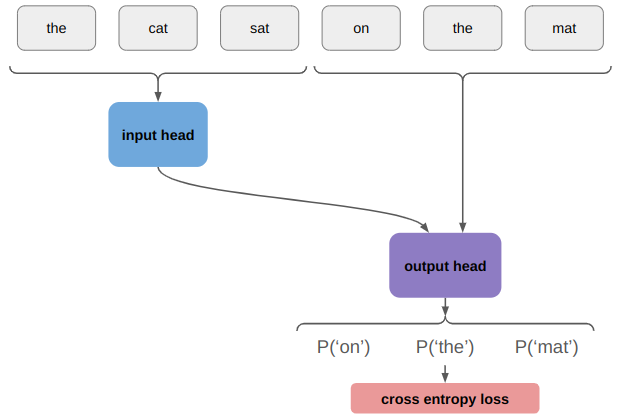
The training that I’ve done so far has all been with teacher forcing, which allows all inputs to be passed to the net at once:
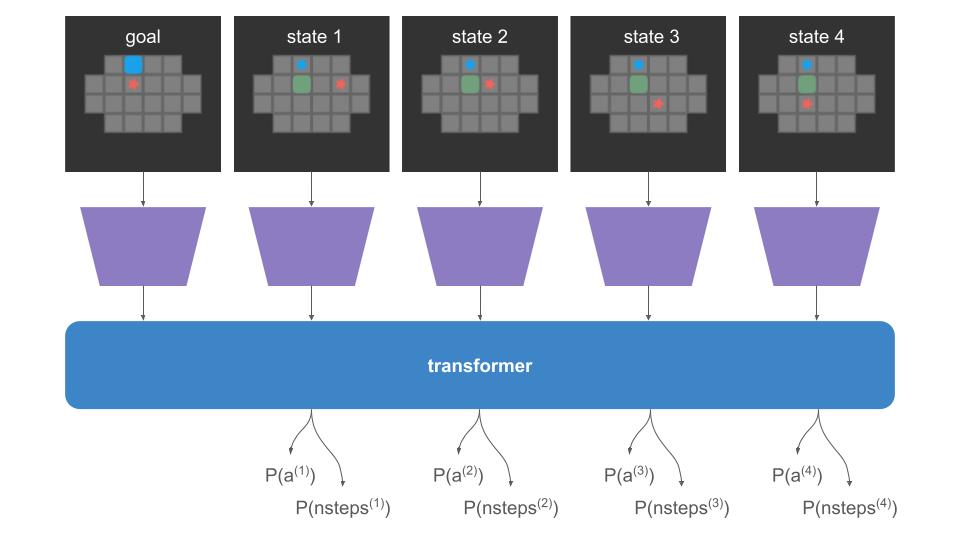
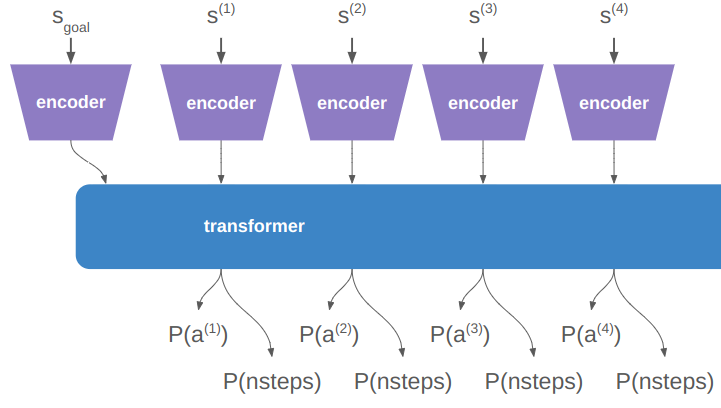
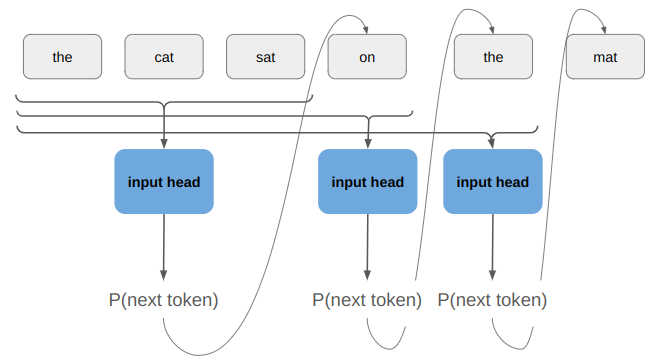
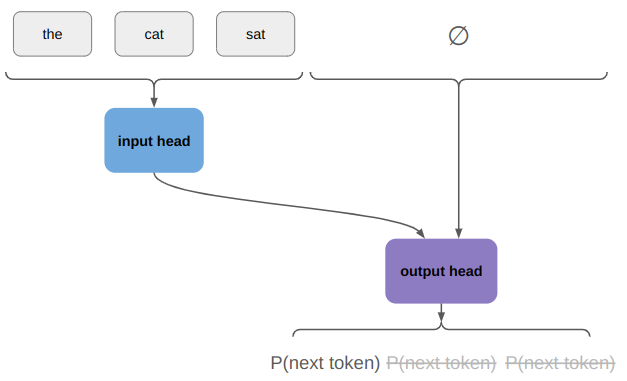
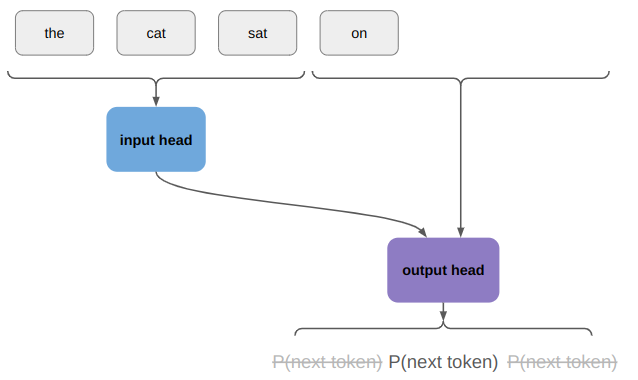
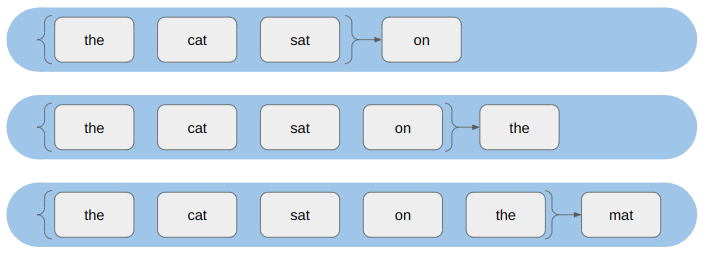
When we do a rollout, we can’t pass everything in at once. We start with our initial state and use the policy to discover where we end up:
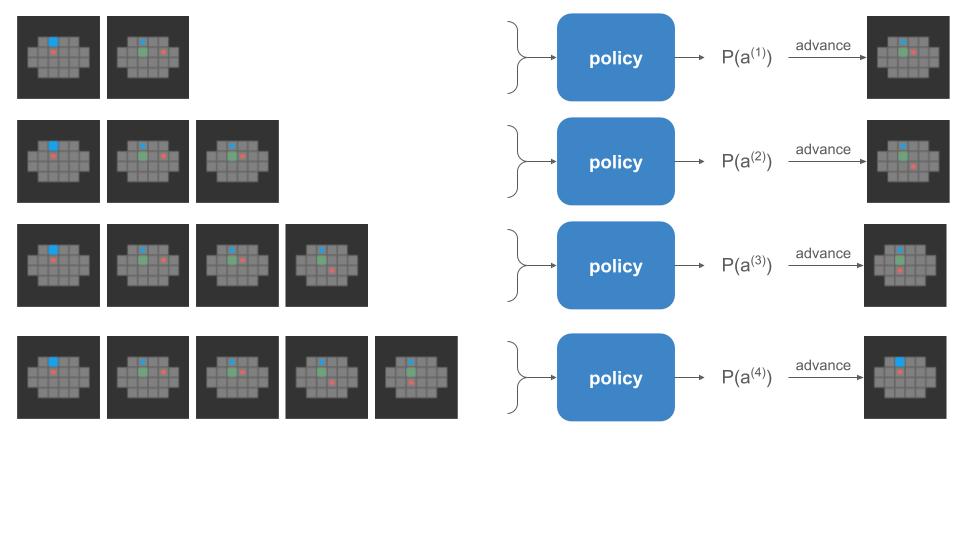
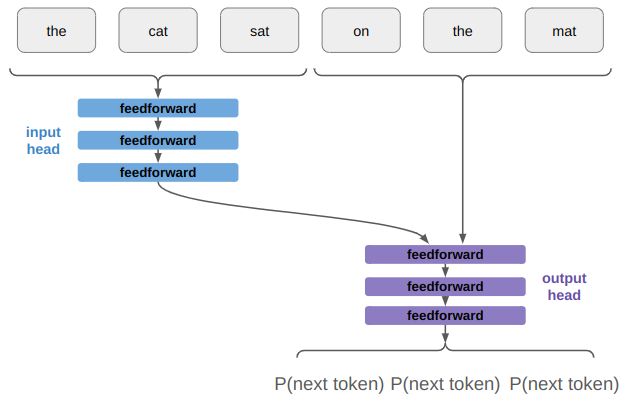
The problem is that the left-side of that image, the policy call, is happening on the GPU, but the right side, the state advancement, is happening on the CPU. If a rollout involves 62 player steps, then instead of one data transfer step like we have for training, we’re doing 61 transfers! Our bottleneck is all that back-and-forth communication:

Let’s move everything to the GPU.
CPU Code
So what is currently happening on the CPU?
At every state, we are:
- Sampling an action for each board from the action logits
- Applying that action to each board to advance the state
Sampling from the actions is pretty straightforward to run on the GPU. That’s the bread and butter of transformers and RL in general.
# policy_logits are [a×s×b] (a=actions, s=sequence length, b = batch size)
policy_logits, nsteps_logits = policy(inputs)
# Sample from the logits using the Gumbel-max trick
sampled_actions = argmax(policy_logits .+ gumbel_noise, dims=1)where we use the Gumbel-max trick and the Gumble noise is sampled in advance and passed to the GPU like the other inputs:
using Distributions.jl
gumbel_noise = rand(Gumbel(0, 1), size(a, s, b))Advancing the board states is more complicated. Here is the CPU method for a single state:
function maybe_move!(board::Board, dir::Direction)::Bool
□_player::TileValue=find_player_tile(board)
step_fore = get_step_fore(board, dir)
□ = □_player # where the player starts
▩ = □ + step_fore # where the player potentially ends up
if is_set(board[▩], WALL)
return false # We would be walking into a wall
end
if is_set(board[▩], BOX)
# We would be walking into a box.
# This is only a legal move if we can push the box.
◰ = ▩ + step_fore # where box ends up
if is_set(board[◰], WALL + BOX)
return false # We would be pushing the box into a box or wall
end
# Move the box
board[▩] &= ~BOX # Clear the box
board[◰] |= BOX # Add the box
end
# At this point we have established this as a legal move.
# Finish by moving the player
board[□] &= ~PLAYER # Clear the player
board[▩] |= PLAYER # Add the player
return true
endThere are many ways to represent board states. This representation is a simple Matrix{UInt8}, so an 8×8 board is just an 8×8 matrix. Each tile is a bitfield with components that can be set for whether that tile has/is a wall, box, floor, or tile.
Moving the player has 3 possible paths:
- successful step: the destination tile is empty and we just move the player to it
- successful push: the destination tile has a box, and the next one over is empty, so we move both the player and the box
- failed move: otherwise, this is an illegal move and the player stays where they are
Moving this logic to the GPU has to preserve this flow, use the GPU’s representation of the board state, and handle a tensor’s worth of board states at a time.
GPU Representation
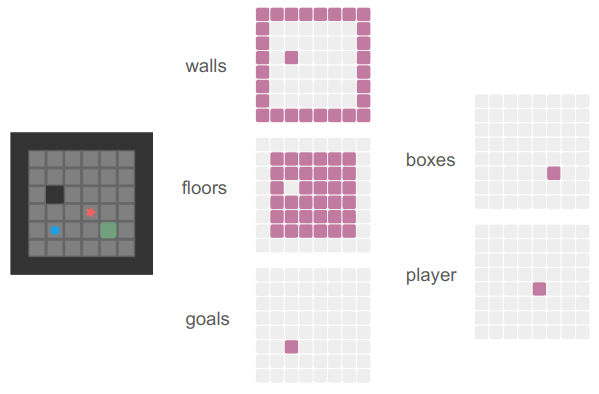
The input to the policy is a tensor of size \([h \times w \times f \times s \times b]\), where 1 board is encoded as a sparse \((h = \text{height}) \times (w=\text{width}) \times (f = \text{num features} = 5)\)
and we have board sequences of length \(s\) and \(b\) sequences per batch of them:
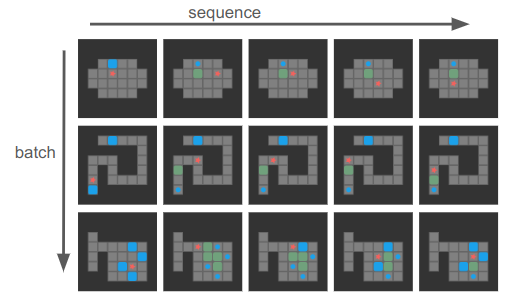
I purposely chose 4-step boards here, but sequences can generally be much longer and of different lengths, and the first state in each sequence is the goal state.
Our actions will be the \([4\times s \times b]\) actions tensor — one up/down/left/right action per board state.
Shifting Tensors
The first fundamental operation we’re going to need is to be able to check tile neighbors. That is, instead of doing this:
□ = □_player # where the player starts
▩ = □ + step_fore # where the player potentially ends upwe’ll be shifting all tiles over and checking that instead:

is_player_dests = shift_tensor(is_players, d_row=0, d_col=1)The shift_tensor method method takes in a tensor and shifts it by the given number of rows and columns, padding in new values:
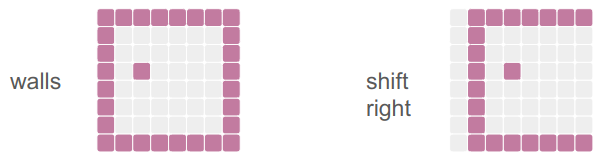
We pass in the number of rows or columns to shift, figure out what that means in terms of padding, and then leverage NNlib’s pad_constant method to give us a new tensor that we clamp to a new range:
function shift_tensor(
tensor::AbstractArray,
d_row::Integer,
d_col::Integer,
pad_value)
pad_up = max( d_row, 0)
pad_down = max(-d_row, 0)
pad_left = max( d_col, 0)
pad_right = max(-d_col, 0)
tensor_padded = NNlib.pad_constant(
tensor,
(pad_up, pad_down, pad_left, pad_right,
(0 for i in 1:2*(ndims(tensor)-2))...),
pad_value)
dims = size(tensor_padded)
row_lo = 1 + pad_down
row_hi = dims[1] - pad_up
col_lo = 1 + pad_right
col_hi = dims[2] - pad_left
return tensor_padded[row_lo:row_hi, col_lo:col_hi,
(Colon() for d in dims[3:end])...]
endThis method works on tensors with varying numbers of dimensions, and always operates on the first two dimensions as the row and column dimensions.
Taking Actions
If we know the player move, we can use the appropriate shift direction to get the “next tile over”. Our player moves can be reflected by the following row and column shift values:
UP = (d_row=-1, d_col= 0)
LEFT = (d_row= 0, d_col=-1)
DOWN = (d_row=+1, d_col= 0)
RIGHT = (d_row= 0, d_col=+1)
This lets us convert the CPU-movement code into a bunch of Boolean tensor operations:
function advance_boards(
inputs::AbstractArray{Bool}, # [h,w,f,s,b]
d_row::Integer,
d_col::Integer)
boxes = inputs[:,:,DIM_BOX, :,:]
player = inputs[:,:,DIM_PLAYER,:,:]
walls = inputs[:,:,DIM_WALL, :,:]
player_shifted = shift_tensor(player, d_row, d_col, false)
player_2_shift = shift_tensor(player_shifted, d_row, d_col, false)
# A move is valid if the player destination is empty
# or if its a box and the next space over is empty
not_box_or_wall = .!(boxes .| walls)
# 1 if it is a valid player destination tile for a basic player move
move_space_empty = player_shifted .& not_box_or_wall
# 1 if the tile is a player destination tile containing a box
move_space_isbox = player_shifted .& boxes
# 1 if the tile is a player destination tile whose next one over
# is a valid box push receptor
push_space_empty = player_shifted .& shift_tensor(not_box_or_wall, -d_row, -d_col, false)
# 1 if it is a valid player move destination
move_mask = move_space_empty
# 1 if it is a valid player push destination
# (which also means it currently has a box)
push_mask = move_space_isbox .& push_space_empty
# new player location
mask = move_mask .| push_mask
player_new = mask .| (player .* shift_tensor(.!mask, -d_row, -d_col, false))
# new box location
box_destinations = shift_tensor(boxes .* push_mask, d_row, d_col, false)
boxes_new = (boxes .* (.!push_mask)) .| box_destinations
return player_new, boxes_new
endThe method appropriately moves any player tile that has an open space in the neighboring tile, or any player tile that has a neighboring pushable box. We create both a new player tensor and a new box tensor.
This may seem extremely computationally expensive — we’re operating on all tiles rather than on just the ones we care about. But GPUs are really good at exactly this, and it is much cheaper to let the GPU churn through that than wait for the transfer to/from the CPU.
The main complication here is that we’re using the same action across all boards. In a given instance, there are \(s\times b\) boards in our tensor. We don’t want to be using the same action in all of them.
Instead of sharding different actions to different boards, we’ll compute the results of all 4 actions and then index into the resulting state that we need:
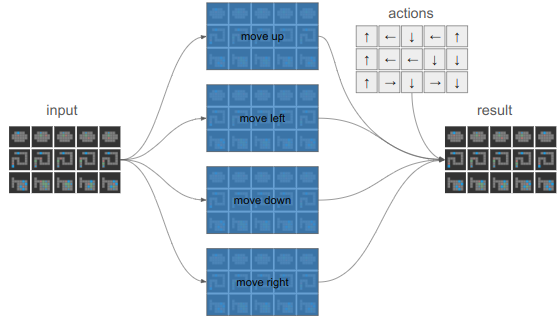
Working with GPUs sure makes you think differently about things.
function advance_boards(
inputs::AbstractArray{Bool}, # [h,w,f,s,b]
actions::AbstractArray{Int}) # [s,b]
succ_u = advance_boards(inputs, -1, 0) # [h,w,s,d], [h,w,s,d]
succ_l = advance_boards(inputs, 0, -1)
succ_d = advance_boards(inputs, 1, 0)
succ_r = advance_boards(inputs, 0, 1)
size_u = size(succ_u[1])
target_dims = (size_u[1], size_u[2], 1, size_u[3:end]...)
player_news = cat(
reshape(succ_u[1], target_dims),
reshape(succ_l[1], target_dims),
reshape(succ_d[1], target_dims),
reshape(succ_r[1], target_dims), dims=3) # [h,w,a,s,d]
box_news = cat(
reshape(succ_u[2], target_dims),
reshape(succ_l[2], target_dims),
reshape(succ_d[2], target_dims),
reshape(succ_r[2], target_dims), dims=3) # [h,w,a,s,d]
actions_onehot = onehotbatch(actions, 1:4) # [a,s,d]
actions_onehot = reshape(actions_onehot, (1,1,size(actions_onehot)...)) # [1,1,a,s,d]
boxes_new = any(actions_onehot .& box_news, dims=3)
player_new = any(actions_onehot .& player_news, dims=3)
return cat(inputs[:,:,1:3,:,:], boxes_new, player_new, dims=3)
endWe’re almost there. This updates the boards in-place. To get the new inputs tensor, we want to shift our boards in the sequence dimension, propagating successor boards to the next sequence index. However, we can’t just shift the entire tensor. We want to keep the goals and the initial states:
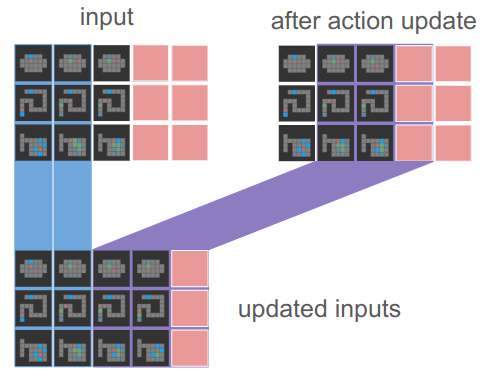
The code for this amounts to a cat operation and some indexing:
function advance_board_inputs(
inputs::AbstractArray{Bool}, # [h,w,f,s,b]
actions::AbstractArray{Int}) # [s,b]
inputs_new = advance_boards(inputs, actions)
# Right shift and keep the goal and starting state
return cat(inputs[:, :, :, 1:2, :],
inputs_new[:, :, :, 2:end-1, :], dims=4) # [h,w,f,s,b]
endAnd with that, we’re processing actions across entire batches!
Rollouts on the GPU
We can leverage this new propagation code to propagate our inputs tensor during a rollout. The policy and the inputs have to be on the GPU, which in Flux.jl can be done with gpu(policy). Note that this requires a CUDA-compatible GPU.
A single iteration is then:
# Run the model
# policy_logits are [4 × s × b]
# nsteps_logits are [7 × s × b]
policy_logits_gpu, nsteps_logits_gpu = policy0(inputs_gpu)
# Sample from the action logits using the Gumbel-max trick
actions_gpu = argmax(policy_logits_gpu .+ gumbel_noise_gpu, dims=1)
actions_gpu = getindex.(actions_gpu, 1) # Int64[1 × s × b]
actions_gpu = dropdims(actions_gpu, dims=1) # Int64[s × b]
# Apply the actions
inputs_gpu = advance_board_inputs(inputs_gpu, actions_gpu)The overall rollout code just throws this into a loop and does some setup:
function rollouts!(
inputs::Array{Bool, 5}, # [h×w×f×s×b]
gumbel_noise::Array{Float32, 3}, # [4×s×b]
policy0::SokobanPolicyLevel0,
s_starts::Vector{Board}, # [b]
s_goals::Vector{Board}) # [b]
policy0 = gpu(policy0)
h, w, f, s, b = size(inputs)
@assert length(s_starts) == b
@assert length(s_goals) == b
# Fill the goals into the first sequence channel
for (bi, s_goal) in enumerate(s_goals)
set_board_input!(inputs, s_goal, 1, bi)
end
# Fill the start states in the second sequence channel
for (bi, s_start) in enumerate(s_starts)
set_board_input!(inputs, s_start, 2, bi)
end
inputs_gpu = gpu(inputs)
gumbel_noise_gpu = gpu(gumbel_noise)
for si in 2:s-1
# Run the model
# policy_logits are [4 × s × b]
# nsteps_logits are [7 × s × b]
policy_logits_gpu, nsteps_logits_gpu = policy0(inputs_gpu)
# Sample from the action logits using the Gumbel-max trick
actions_gpu = argmax(policy_logits_gpu .+ gumbel_noise_gpu, dims=1)
actions_gpu = getindex.(actions_gpu, 1) # Int64[1 × s × b]
actions_gpu = dropdims(actions_gpu, dims=1) # Int64[s × b]
# Apply the actions
inputs_gpu = advance_board_inputs(inputs_gpu, actions_gpu)
end
return cpu(inputs_gpu)
endThere are several differences:
- The code is simpler. We only have a single loop, over the sequence length (number of steps to take). The content of that loop is pretty compact.
- The code does more work. We’re processing more stuff, but because it happens in parallel on the GPU, its okay. We’re also propagating all the way to the end of the sequence whether we need to or not. (The CPU code would check whether all boards had finished already).
If we time how long it takes to doing a batch worth of rollouts before and after moving to the GPU, we get about a \(60\times\) speedup. Our efforts have been worth it!
Beam Search on the GPU
Rollouts aren’t the only thing we want to speed up. I want to use beam search to explore the space using the policy and try to find solutions. Rollouts might happen to find solutions, but beam search should be a lot better.
The code ends up being basically the same, except a single goal and board is used to seed the entire batch (giving us a number of beams equal to the batch size), and we have to do some work to score the beams and then select which ones to keep:
unction beam_search!(
inputs::Array{Bool, 5}, # [h×w×f×s×b]
policy0::SokobanPolicyLevel0,
s_start::Board,
s_goal::Board)
policy0 = gpu(policy0)
h, w, f, s, b = size(inputs)
# Fill the goals and starting states into the first sequence channel
for bi in 1:b
set_board_input!(inputs, s_goal, 1, bi)
set_board_input!(inputs, s_start, 2, bi)
end
# The scores all start at zero
beam_scores = zeros(Float32, 1, b) |> gpu # [1, b]
# Keep track of the actual actions
actions = ones(Int, s, b) |> gpu # [s, b]
inputs_gpu = gpu(inputs)
# Advance the games in parallel
for si in 2:s-1
# Run the model
# policy_logits are [4 × s × b]
# nsteps_logits are [7 × s × b]
policy_logits, nsteps_logits = policy0(inputs_gpu)
# Compute the probabilities
action_probs = softmax(policy_logits, dims=1) # [4 × s × b]
action_logls = log.(action_probs) # [4 × s × b]
# The beam scores are the running log likelihoods
action_logls_si = action_logls[:, si, :] # [4, b]
candidate_beam_scores = action_logls_si .+ beam_scores # [4, b]
candidate_beam_scores_flat = vec(candidate_beam_scores) # [4b]
# Get the top 'b' beams
topk_indices = partialsortperm(candidate_beam_scores_flat, 1:b; rev=true)
# Convert flat indices back to action and beam indices
selected_actions = (topk_indices .- 1) .÷ b .+ 1 # [b] action indices (1 to 4)
selected_beams = (topk_indices .- 1) .% b .+ 1 # [b] beam indices (1 to b)
selected_scores = candidate_beam_scores_flat[topk_indices] # [b]
inputs_gpu = inputs_gpu[:,:,:,:,selected_beams]
actions[si,:] = selected_actions
# Apply the actions to the selected beams
inputs = advance_board_inputs(inputs_gpu, actions)
end
return (cpu(inputs_gpu), cpu(actions))
endThis again results in what looks like way simpler code. The beam scoring and such is all done on tensors, rather than a bunch of additional for loops. It all happens on the GPU, and it is way faster (\(23\times\)).
Conclusion
The previous blog post was about leveraging the GPU during training. This blog post was about leveraging the GPU during inference. We had to avoid expensive data transfers between the CPU and the GPU, and to achieve that had to convert non-trivial player movement code to computations amenable to the GPU. Going about that meant thinking about and structuring our code very differently, working across tensors and creating more work that the GPU could nonetheless complete faster.
This post was a great example of how code changes based on the scale you’re operating at. Peter van Hardenberg gives a great talk about similar concepts in Why Can’t We Make Simple Software?. How you think about a problem changes a lot based on problem scale and hardware. Now that we’re graduating from the CPU to processing many many boards, we have to think about the problem differently.
Our inference code has been GPU-ized, so we can leverage it to speed up validation and solution search. It was taking me 20 min to train a network but 30 min to run beam search on all boards in my validation set. This change avoids that sorry state of affairs.