This post expands on the previous post, which looked at collision detection and resolution for 2d polygons. By the end we were able to apply impulses to colliding bodies to properly get them to bounce and spin off of one another. Not only will we take it further with friction impulses and joints, but we’ll pay special attention to how these impulses are derived to emphasize that this line of reasoning is a tool that can be extended to new applications.
There is more math in this post than normal because I want to both provide a resource that I myself could have benefited from and show that this stuff can all be derived.
An impulse \(\boldsymbol{j}\) is an instantaneous change in momentum. They are very similar to forces, which influence velocity over time:
\[\boldsymbol{f} = m \boldsymbol{a} \quad \Rightarrow \quad \boldsymbol{v}’ \approx \boldsymbol{v} + \frac{1}{m} \boldsymbol{f} \Delta t\]
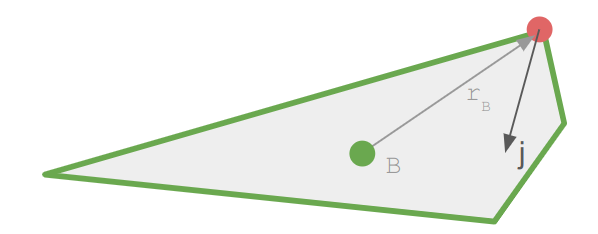
An impulse applied to a rigid body at a point \(\boldsymbol{r}\) relative to the body’s center of mass similarly affects its velocity, but without the need for the timestep:
\[\boldsymbol{v}’ = \boldsymbol{v} + \frac{1}{m} \boldsymbol{j}\]
This impulse also effects the angular velocity:
\[\boldsymbol{\omega}’ = \boldsymbol{\omega} + \boldsymbol{I}^{-1} \boldsymbol{r} \times \boldsymbol{j}\]
This update models the angular velocity in three dimensions, treating it as a vector. We can work out the equivalent 2d update where we just keep track of a scalar \(\omega\):
\[\begin{align}\boldsymbol{r} \times \boldsymbol{j} = \begin{bmatrix} r_x \\ r_y \\ 0\end{bmatrix}\end{align} \times \begin{bmatrix}j_x \\ j_y \\ 0\end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ r_x j_y – r_y j_x \end{bmatrix}\]
If we assume our inertia tensor is diagonal, and just pull out the z entry \(I_{zz}\), we get:
\[\omega’ = \omega + \frac{1}{I_{zz}} \left(r_x j_y – r_y j_x\right)\]
From here on out, if you see a scalar \(I\), it refers to \(I_zz\).
The Normal Impulse
In the last blog post, we used an impulse along the impact normal to cause two colliding rigid bodies to bounce off each other. We’re going to cover the same thing, but derive it instead of just take the result for granted.
We have two bodies, A and B, and a contact point located at \(\boldsymbol{r}_A\) relative to body A’s center and at \(\boldsymbol{r}_B\) relative to body B’s center:
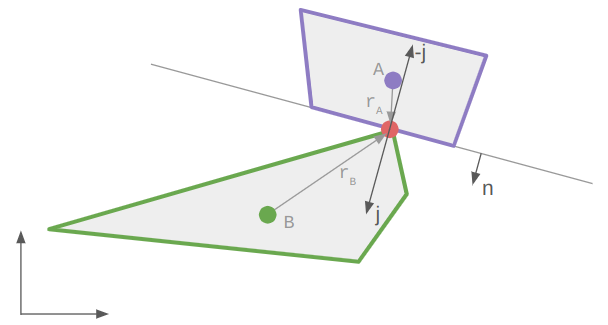
The velocity of the contact points on each body as they enter the collision is:
\[\begin{align}\boldsymbol{v}_{cA} & = \boldsymbol{v}_A + \boldsymbol{\omega}_A \times \boldsymbol{r}_A \\ \boldsymbol{v}_{cB} &= \boldsymbol{v}_B + \boldsymbol{\omega}_B \times \boldsymbol{r}_B \end{align}\]
In 2D that amounts to:
\[\boldsymbol{v}_{cA} = \begin{bmatrix}v_{A,x} \\ v_{A,y} \\ 0\end{bmatrix} + \begin{bmatrix}0 \\ 0 \\ \omega_A\end{bmatrix} \times \begin{bmatrix} r_{A,x} \\ r_{A,y} \\ 0\end{bmatrix} = \begin{bmatrix}v_{A,x} \\ v_{A,y} \\ 0\end{bmatrix} + \begin{bmatrix}-\omega r_{A,y} \\ \hphantom{-}\omega r_{A,x} \\ 0\end{bmatrix} \]
One can do this stuff in 3D and then drop or ignore the \(z\)-axis, but in my code I just stick with 2D:
Vec2f r; // radius
Vec2f v; // linear velocity vector
f32 w; // angular velocity
Vec2f v_c = v + w * Rotr(r);The contact velocity — how fast the contact points collide — is the relative speed of the contact points:
\[\boldsymbol{v}_\text{rel} = \boldsymbol{v}_{cB} \> – \boldsymbol{v}_{cA}\]
To derive the impulse, we stipulate two things. First, that the impulse lies in the normal direction:
\[\boldsymbol{j} = j \hat{\boldsymbol{n}}\]
Second, that the relative velocity along the normal direction reverses sign and changes by a factor \(e\):
\[\boldsymbol{v}_\text{rel}’ \cdot \hat{\boldsymbol{n}} = \> – e \> \boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{n}}\]
This factor \(e\) is called the restitution. Setting it to zero produces a perfectly inelastic collision (because the resulting relative velocity in the normal direction is zero), whereas setting it to 1 produces a perfectly elastic collision that preserves the kinetic energy. Most objects use a value somewhere in-between.
We now have everything we need to derive the impulse. Let’s expand the left-hand side of the restitution equation:
\[\begin{align}\boldsymbol{v}_\text{rel}’ \cdot \hat{\boldsymbol{n}} \\ \left(\boldsymbol{v}_{cB}’ \> – \boldsymbol{v}_{cA}’\right) \cdot \hat{\boldsymbol{n}} \\ \left[\left(\boldsymbol{v}_B’ + \boldsymbol{\omega}_B’ \times \boldsymbol{r}_B\right) – \left(\boldsymbol{v}_A’ + \boldsymbol{\omega}_A’ \times \boldsymbol{r}_A\right)\right] \cdot \hat{\boldsymbol{n}} \\ \left[\left(\left[\boldsymbol{v}_B + \frac{1}{m_B}\boldsymbol{j}\right] + \left[\boldsymbol{\omega}_B + \boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \boldsymbol{j}\right] \times \boldsymbol{r}_B\right) – \left(\left[\boldsymbol{v}_A – \frac{1}{m_A}\boldsymbol{j}\right] + \left[\boldsymbol{\omega}_A – \boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \boldsymbol{j}\right] \times \boldsymbol{r}_A\right)\right] \cdot \hat{\boldsymbol{n}} \\ \left[\left(\left[\boldsymbol{v}_B + j \frac{1}{m_B}\hat{\boldsymbol{n}}\right] + \left[\boldsymbol{\omega}_B + j \boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_B\right) – \left(\left[\boldsymbol{v}_A – j \frac{1}{m_A}\hat{\boldsymbol{n}}\right] + \left[\boldsymbol{\omega}_A – j \boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_A\right)\right] \cdot \hat{\boldsymbol{n}} \\ \left[\boldsymbol{v}_\text{rel} + j \left(\frac{1}{m_B}\hat{\boldsymbol{n}} + \left[ \boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_B + \frac{1}{m_A}\hat{\boldsymbol{n}} + \left[ \boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_A\right)\right] \cdot \hat{\boldsymbol{n}} \\ \boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{n}} + j \left(\frac{1}{m_A}\hat{\boldsymbol{n}} + \frac{1}{m_B}\hat{\boldsymbol{n}} + \left[ \boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_A + \left[ \boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_B\right) \cdot \hat{\boldsymbol{n}} \\ \boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{n}} + j \left(\frac{1}{m_A}\hat{\boldsymbol{n}}\cdot \hat{\boldsymbol{n}} + \frac{1}{m_B}\hat{\boldsymbol{n}}\cdot \hat{\boldsymbol{n}} + \left[ \boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_A \cdot \hat{\boldsymbol{n}} + \left[ \boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_B \cdot \hat{\boldsymbol{n}}\right) \\ \boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{n}} + j \left(\frac{1}{m_A} + \frac{1}{m_B} + \left[ \boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_A \cdot \hat{\boldsymbol{n}} + \left[ \boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_B \cdot \hat{\boldsymbol{n}}\right) \end{align}\]
We then equate this to \( – e \> \boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{n}}\) and solve for the impulse scalar \(j\), yielding:
\[j = \frac{-(1+e) \boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{n}} }{ \frac{1}{m_A} + \frac{1}{m_B} + \left(\left[ \boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_A + \left[ \boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \hat{\boldsymbol{n}}\right] \times \boldsymbol{r}_B\right) \cdot \hat{\boldsymbol{n}} }\]
This is the equation that Wikipedia gives us.
The equation I gave in the last blog post looks a little different:
\[j = \frac{-(1+e)\boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{n}}}{\frac{1}{m_A} + \frac{1}{m_B} + \frac{(\boldsymbol{r}_A \times \boldsymbol{n})^2}{I_A} + \frac{(\boldsymbol{r}_B \times \boldsymbol{n})^2}{I_B}}\]
It only differs in the terms involving the moment of inertia.
Let’s expand the Wikipedia version:
\[\begin{align}\left[\left(\boldsymbol{I}^{-1} \boldsymbol{r} \times \hat{\boldsymbol{n}}\right) \times \boldsymbol{r}\right] \cdot \hat{\boldsymbol{n}} &= \left(\left(\frac{1}{I}\begin{bmatrix}r_x \\ r_y \\ 0\end{bmatrix} \times \begin{bmatrix} \hat{n}_x \\ \hat{n}_y \\ 0 \end{bmatrix}\right) \times \begin{bmatrix}r_x \\ r_y \\ 0\end{bmatrix}\right) \cdot \begin{bmatrix}\hat{n}_x \\ \hat{n}_y \\ 0\end{bmatrix} \\ &= \left(\frac{1}{I}\begin{bmatrix}0 \\ 0 \\ r_x \hat{n}_y – r_y \hat{n}_x\end{bmatrix} \times \begin{bmatrix}r_x \\ r_y \\ 0\end{bmatrix}\right) \cdot \begin{bmatrix}\hat{n}_x \\ \hat{n}_y \\ 0\end{bmatrix} \\ &= \frac{1}{I}\begin{bmatrix}-r_x r_y \hat{n}_y + r_y^2 \hat{n}_x \\ r_x^2 \hat{n}_y – r_x r_y \hat{n}_x \\ 0 \end{bmatrix} \cdot \begin{bmatrix}\hat{n}_x \\ \hat{n}_y \\ 0\end{bmatrix} \\ &= \frac{1}{I}\left( r_x^2 \hat{u}_y^2 – 2 r_x r_y \hat{u}_x \hat{u}_y + r_y^2 \hat{u}_y^2 \right) \end{align}\]
We get the same thing if we expand the other version:
\[\begin{align}\frac{1}{I}\left(\boldsymbol{r} \times \hat{\boldsymbol{n}}\right)^2 &= \frac{1}{I}\left(r_x \hat{n}_y – r_y \hat{n}_x\right)^2 \\ &= \frac{1}{I}\left( r_x^2 \hat{u}_y^2 – 2 r_x r_y \hat{u}_x \hat{u}_y + r_y^2 \hat{u}_y^2 \right)\end{align}\]
The two formulations are equal, but assume that we’re working in 2D and that the moment of inertia tensor is diagonal with every entry equal to \(I\). The Wikipedia version is more general, and can handle 3D collisions and general inertia tensors.
The normal impulse \(j\) in 2D is thus
\[j = \> -(1+e) \> m_\text{eff} \> \boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{n}} \]
where the effective mass is
\[m_\text{eff} = \left(\frac{1}{m_A} + \frac{1}{m_B} + \frac{(\boldsymbol{r}_A \times \hat{\boldsymbol{n}})^2}{I_A} + \frac{(\boldsymbol{r}_B \times \hat{\boldsymbol{n}})^2}{I_B}\right)^{-1}\]
After calculating it, we apply an impulse \(j \hat{\boldsymbol{n}}\) to body B and the negated impulse to body A. Note that we only apply an impulse if the relative velocity is causing the bodies to move into contact (\(\boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{n}} < 0\)), otherwise the contact point already has a separating velocity.
The restitution \(e\) will depend on the colliding bodies. One convenient way to get it is to assign an restitution to each rigid body, and then use the maximum between the two for the collision. That allows bounciness to win out:
\[e = \max\left(e_A, e_B\right)\]
Friction Impulse
The normal impulse takes care of the relative penetration speed, but does nothing in the tangent direction along the contact line. We typically want shapes that slide along each other to have friction — that is what the friction impulse, or tangent impulse, is for.
Wikipedia and other websites will at this point show you a fancy diagram for Coulomb friction depicting the friction cone. I don’t find that to be particularly illuminating.
Instead, I simply like to think about Coulomb friction as:
- compute a tangent impulse that causes the relative tangent velocity to be zero (\(e=0\))
- if the required tangent impulse is sufficiently small, apply it (static friction)
- if the required tangent impulse is too large, cap it out and apply that instead (dynamic friction)
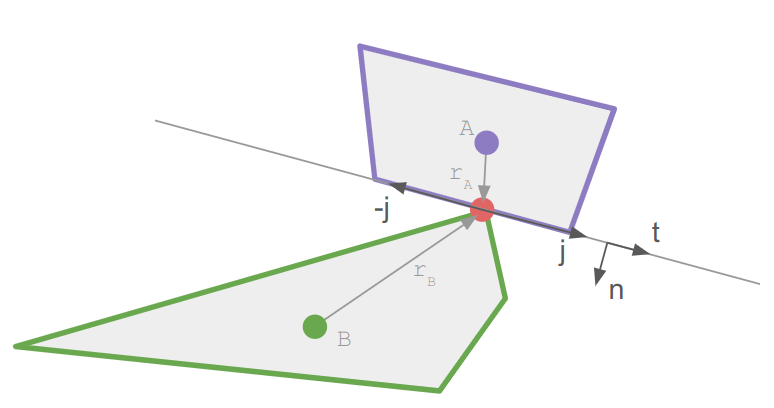
Let’s derive the update ourselves again.
The friction impulse acts in the tangent direction \(\hat{\boldsymbol{t}}\), which we can get by rotating the normal. We once again have a scalar impulse:
\[j = j \hat{\boldsymbol{t}}\]
We compute the tangent that causes a zero relative tangent velocity (\(e = 0\)).
These two conditions are structurally the same as the normal impulse, except \(e\) is fixed. We can directly apply our previous equations to get:
\[j = \> – m_\text{eff} \> \boldsymbol{v}_\text{rel} \cdot \hat{\boldsymbol{t}}\]
where the effective mass is now in the tangent direction:
\[m_\text{eff} = \left(\frac{1}{m_A} + \frac{1}{m_B} + \frac{(\boldsymbol{r}_A \times \hat{\boldsymbol{t}})^2}{I_A} + \frac{(\boldsymbol{r}_B \times \hat{\boldsymbol{t}})^2}{I_B}\right)^{-1}\]
As long as this impulse is small enough (in magnitude), we apply it in order to prevent any tangential sliding. If it is large enough, we switch from static friction to dynamic friction:
\[j = \begin{cases} j & \text{if } |j| \leq j_\text{static} \\ j_\text{dynamic} & \text{otherwise} \end{cases}\]
Easy peasy.
The static and dynamic friction values are typically multiples of the normal impulse. We multiply the normal impulse by \(\mu_\text{static}\) to get the static friction impulse threshold and by \(\mu_\text{dynamic}\) to get the dynamic friction impulse threshold. Like the restitution, these are properties of each body, and we can obtain values to use for a pair of bodies by combining their values. Here it is recommended to use the square root of the product, which lets extremely low-friction (slippery) values dominate:
\[\mu_\text{static} = \sqrt{\vphantom{P}\mu_{A,\text{static}} \cdot \mu_{B,\text{static}}}\]
Revolute Joints
There are other things we can do with impulses. One of the main ones is to model attachment points between rigid bodies. These revolute joints allow rotation, but force the bodies to maintain a constant distance vector to the joint:
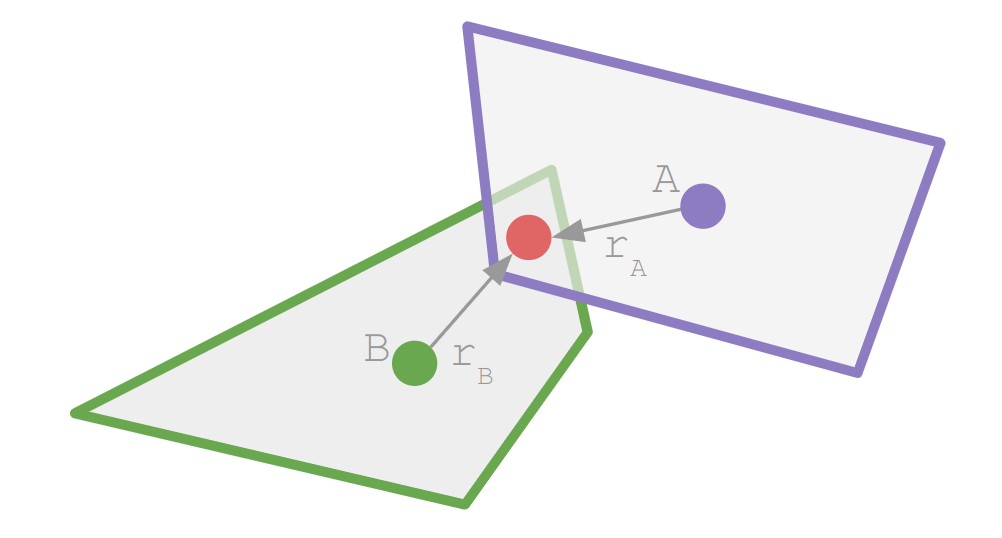
Revolute joints are useful for all sorts of things, including swinging:
I didn’t have a lot of luck finding information on how to enforce revolute joints between rigid bodies in 2D. Thankfully, we can derive the necessary impulse ourselves.
The property we want to enforce is that the contact velocity at the joint after the impulse be zero:
\[\boldsymbol{v}_\text{rel}’ = \boldsymbol{0}\]
We can expand that out:
\[\begin{align}\boldsymbol{v}_\text{rel}’ &= \boldsymbol{0} \\ \boldsymbol{v}_{cB}’ \> – \boldsymbol{v}_{cA}’ &= \boldsymbol{0} \\ \left(\boldsymbol{v}_B’ + \boldsymbol{\omega}_B’ \times \boldsymbol{r}_B\right) – \left(\boldsymbol{v}_A’ + \boldsymbol{\omega}_A’ \times \boldsymbol{r}_A\right) &= \boldsymbol{0} \\ \left(\left[\boldsymbol{v}_B + \frac{1}{m_B}\boldsymbol{j}\right] + \left[\boldsymbol{\omega}_B + \boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \boldsymbol{j}\right] \times \boldsymbol{r}_B\right) – \left(\left[\boldsymbol{v}_A – \frac{1}{m_A}\boldsymbol{j}\right] + \left[\boldsymbol{\omega}_A – \boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \boldsymbol{j}\right] \times \boldsymbol{r}_A\right) &= \boldsymbol{0} \\ \boldsymbol{v}_\text{rel} + \left(\frac{1}{m_B}\boldsymbol{j} + \left[\boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \boldsymbol{j}\right] \times \boldsymbol{r}_B\right) + \left(\frac{1}{m_A}\boldsymbol{j} + \left[\boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \boldsymbol{j}\right] \times \boldsymbol{r}_A\right) &= \boldsymbol{0} \\ \boldsymbol{v}_\text{rel} + \left(\frac{1}{m_A} + \frac{1}{m_B}\right)\boldsymbol{j} + \left(\boldsymbol{I}_A^{-1} \boldsymbol{r}_A \times \boldsymbol{j}\right) \times \boldsymbol{r}_A + \left(\boldsymbol{I}_B^{-1} \boldsymbol{r}_B \times \boldsymbol{j}\right) \times \boldsymbol{r}_B &= \boldsymbol{0}\end{align}\]
If we work out the cross products, then we end up with the following system of equations:
\[\begin{bmatrix}\frac{1}{m_A} + \frac{1}{m_B} + \frac{1}{I_A}r_{Ay}^2 + \frac{1}{I_B}r_{By}^2 & -\left(\frac{1}{I_A}r_{Ax}r_{Ay} + \frac{1}{I_B}r_{Bx}r_{By}\right) \\ -\left(\frac{1}{I_A}r_{Ax}r_{Ay} + \frac{1}{I_B}r_{Bx}r_{By}\right) & \frac{1}{m_A} + \frac{1}{m_B} + \frac{1}{I_A}r_{Ax}^2 + \frac{1}{I_B}r_{Bx}^2\end{bmatrix}\begin{bmatrix} j_x \\ j_y\end{bmatrix} = \begin{bmatrix}-v_{\text{rel},x} \\ -v_{\text{rel},y}\end{bmatrix}\]
We can write a simple function that can solve such a \(2 \times 2\) linear system:
// Solve a 2x2 system of linear equations
// [a b][x1] = [e]
// [c d][x2] = [f]
// This method assumes that it will succeed, which
// requires that the matrix be invertible.
template <typename T>
void Solve(T a, T b, T c, T d, T e, T f, T& x1, T& x2) {
T det = d * a - c * b;
x2 = (a * f - c * e) / det;
x1 = (e - b * x2) / a;
}and then use that to solve for our impulse.
// Compute the effective mass components.
f32 m_eff_11 = inv_m1 + inv_m2 + inv_I1 * r1.y * r1.y + inv_I2 * r2.y * r2.y;
f32 m_eff_12 = -(inv_I1 * r1.x * r1.y + inv_I2 * r2.x * r2.y);
f32 m_eff_22 = inv_m1 + inv_m2 + inv_I1 * r1.x * r1.x + inv_I2 * r2.x * r2.x;
// Solve for the impulse:
// [m_eff_11 m_eff_12][j.x] = [-v_rel.x]
// [m_eff_12 m_eff_22][j.y] = [-v_rel.y]
Vec2f j;
Solve(m_eff_11, m_eff_12, m_eff_12, m_eff_22, -v_rel.x, -v_rel.y, j.x, j.y);We can then apply the resulting impulse to both bodies and perform a positional correction. I weight the correction such that the target joint location is biased toward the heavier object (that way joints on infinite-mass objects never move).
Conclusion
This post set the mathematical foundation for impulses, then derived the normal, friction, and revolute joint impulses. In each case, we looked at what was being preserved, formulated that mathematically, and massaged the equations to back out the impulse. While the equations were long at times, they did not lead us astray and we were able to find our way to some solid physics.