A few weeks ago I got an email asking me about a game I worked on ages ago. I had to inform the sender that, unfortunately, my inspired dreams of creative development had not come to full fruition.
The message did get me thinking. What had I been doing back then, about 8 years ago? What problems did I run into? Why did I stop?
Now, I took a look at my old source code, and I’m pretty sure I stopped because of the mounting complexity of classes and cruft that happens in a growing codebase, especially when one has comparatively little idea of what one is doing. That, and I’m pretty sure this was around the time of my qualification exams, and well, I think that took over my life at the time.
Anyhow, I was thinking about this top-down 2D game, and the thoughts that kept circling around my brain centered around 2D character movement and collision. This was only magnified when I played some iPhone games to supplement my entertainment when I flew long distance over the holidays, and grew dismayed at some of the movement systems. I thought player movement was hard back then, and even today a fair number of games don’t really cut the mustard.
The Problem
So this post is borne out of mulling over this old problem of how to move a player around in a 2D game without them running into things. We want a few things:
- Nice continuous movement
- To not intersect static geometry
- To nicely slide along static geometry
- To not get hung up on edges, and nicely roll around them
And, as bonus objectives, we’d love to:
- Do all of these things efficiently
- Be able to handle non-tile maps with arbitrary geometry
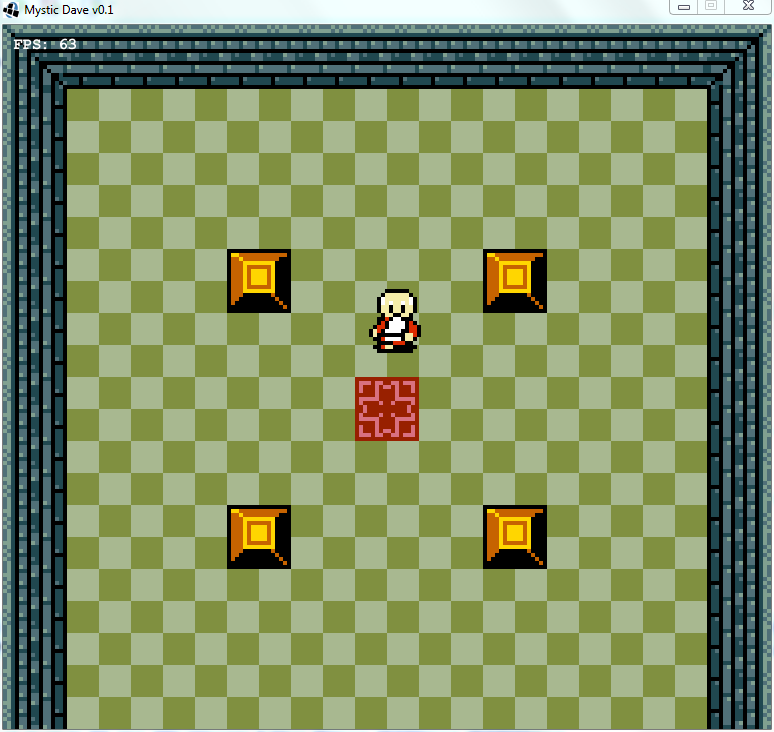
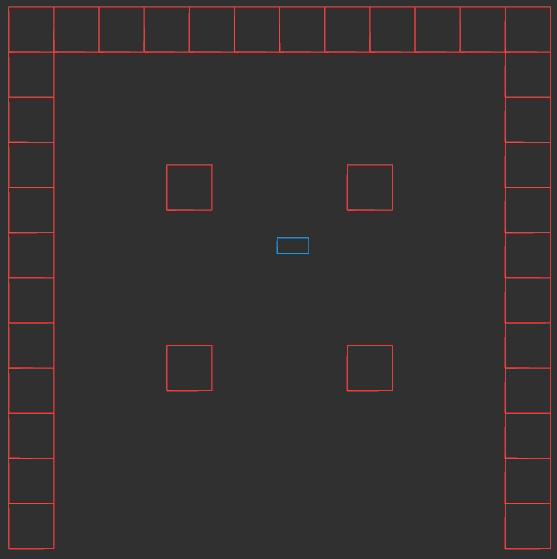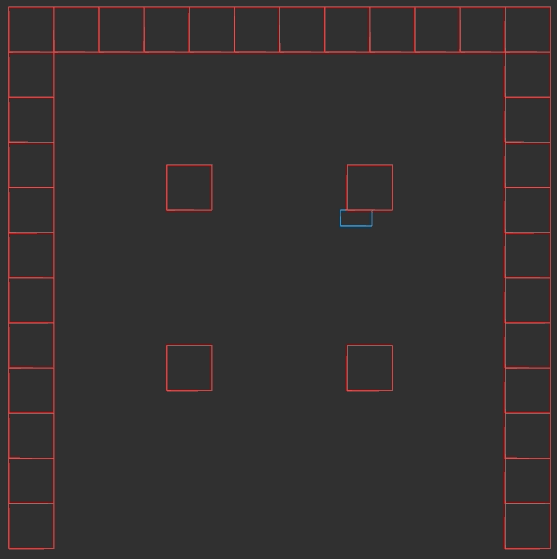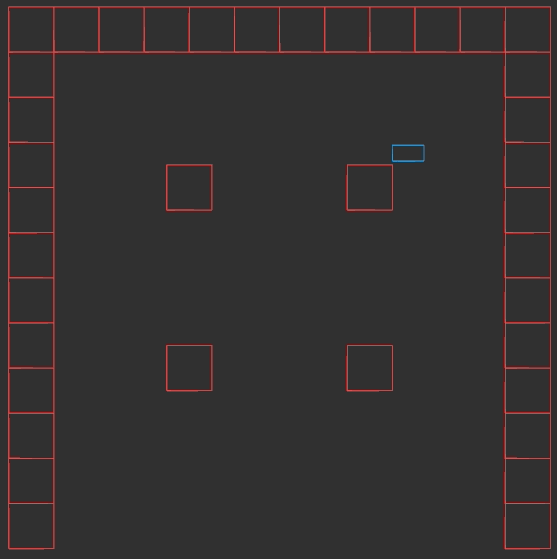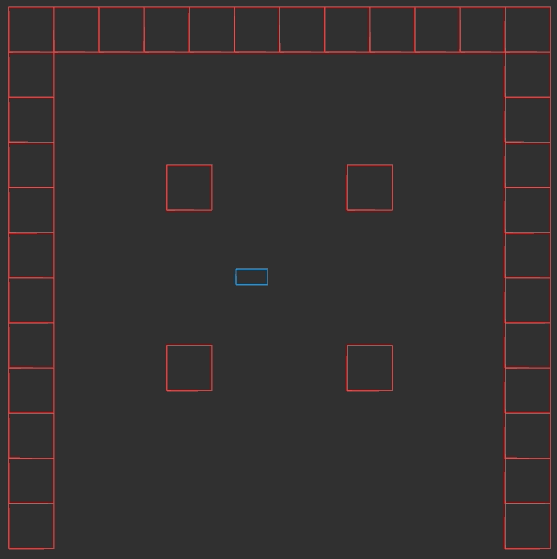
The central issue with many games is that you have things you don’t want to run into. For example, below we have a screenshot from my old game-in-development Mystic Dave. We have a player character (Mystic Dave) and some objects (red) that we don’t want Dave to run into:

The player typically has a collision volume centered on their location. This collision volume is not allowed to intersect with any of the level collision geometry:

So what we’re really dealing with is moving this player collision volume around with the player, and making sure that it doesn’t intersect with anything.
Basic Player Movement
The player movement part is pretty simple. We can just look at whatever direction the player input is getting us to move in, and move ourselves in that direction:
void UpdatePlayer(Vec2 input_dir) {
Vec2 pos_delta = input_dir * kPlayerStepSize;
pos_player_ += pos_delta;
}We’ll run into tuning problems later on if we don’t make this a function of the time step, so let’s go ahead and do that now:
void UpdatePlayer(Vec2 input_dir, float dt) {
Vec2 pos_delta = input_dir * kPlayerStepSizePerTime * dt;
pos_player_ += pos_delta;
}This will give us some pretty basic movement:

That movement is a bit boring. It stutters around.
We can make it smoother by storing the player’s velocity and adding to that instead. We enforce a maximum velocity and apply some air friction to slow the player down as we stop our inputs:
void UpdatePlayer(Vec2 input_dir, float dt) {
// Update the player's velocity
vel_player_ += input_dir * kPlayerInputAccel * dt;
// Clamp the velocity to a maximum magnitude
float speed = Norm(vel_player_);
if (speed > kPlayerMaxSpeed) {
vel_player_ *= kPlayerMaxSpeed / norm;
}
// Update the player's position
Vec2 pos_delta = vel_player_ * dt;
pos_player_ += pos_delta;
// Apply air friction
vel_player_ *= kFrictionAir;
}Alright, now we’re zooming around:

So how do we do the colliding part?
Naive Collision
The way I first approached player collision, way back in the day, was to say “hey, we have a top-down 2D tile-based game, so our collision objects are all squares, and we can just check for collision against squares”. A reasonable place to start.
Okay, so we have a rectangle for our player and consistently-sized squares for all of our static geometry. That can’t be too hard, right?
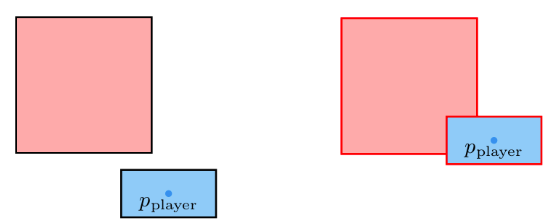
Checking for collisions between axis-aligned rectangles isn’t all that hard. You can use something like the separating axis theorem. A quick Google search gives you code to work with.
Our strategy now is to calculate the new player position, check it against our collision geometry for intersections, and to not move our player if that fails. If we do that, we find that we need (1) to zero out the player’s speed on collision, and (2) we still actually want to move the player, except we want to move them up against the colliding body:
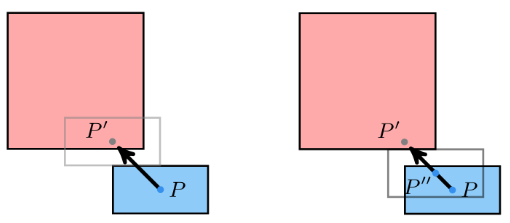
Doing this part is harder. We can do it, but it takes some math. In the case of an axis-aligned rectangle, if we know which side our collision point is closest to, we can just shift our new position \(P’\) out of the closest face by half the player-rect’s width in that axis. The code looks something like:
void UpdatePlayer(Vec2 input_dir, float dt) {
// Update the player's velocity, clamp, etc.
... same as before
// Update the player's position
Vec2 pos_delta = vel_player_ * dt;
pos_player_ += pos_player_ + pos_delta;
Box player_box_next = Box(pos_next, player_height, player_width);
for (const Box& box : collision_objects_) {
auto collision_info = CheckCollision(box, player_box_next)
if (collision_info.collided) {
// Collision!
vel_player_ = Vec2(0,0);
pos_player_ = box.center;
if (collision_info.nearest_side == NORTH) {
pos_player_ += Vec2(0, box.height/2 + player_height/2);
} else if (collision_info.nearest_side == EAST) {
pos_player_ += Vec2(box.width/2 + player_width/2, 0);
} else if (collision_info.nearest_side == SOUTH) {
pos_player_ -= Vec2(0, box.height/2 + player_height/2);
} else if (collision_info.nearest_side == WEST) {
pos_player_ -= Vec2(box.width/2 + player_width/2, 0);
}
}
}
// Apply air friction
vel_player_ *= kFrictionAir;
}So this works, but has some issues. First off, we’re iterating over all boxes. That’s a big inefficiency right off the bat, especially on a large level with a lot of filled tiles. That particular problem is pretty easy to avoid, typically by using a more efficient data structure for keeping track of our collision geometry, like a quad tree for general collision objects and searching around a simple tile-based index for something like Mystic Dave.
Second, we project out of the nearest face. This can lead to all sorts of glitches. If we start on one side of the box, but move such that our closest face is a different one, we get shunted out the wrong side:
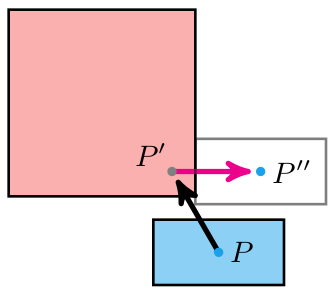
This effect is particularly problematic when we have multiple collision bodies. The code above processes them all in series, which could be totally wrong. We want to collide with the first thing we’d hit first.
Alternatively we could use a while loop, and keep on checking for collisions after we get shunted around by our collision logic, but this could end up causing weird infinite loops:
After we process any collisions, we set the player’s speed to zero. This causes the player to just stop. There is no nice sliding along the surface, let alone nicely rolling around corners:

Thinking in Points
Okay, maybe we can do this differently. Let’s take a step back and refine our problem.
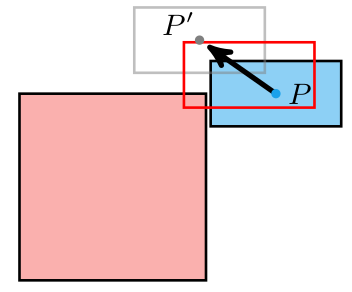
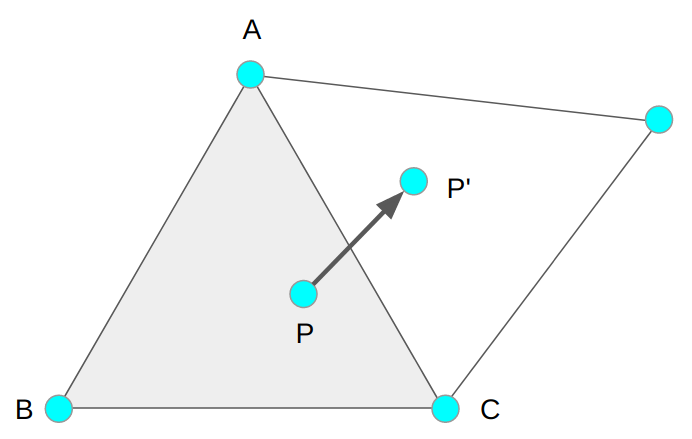
We have a point \(P\), which we are moving a small step to some \(P’\). We assume \(P\) is valid (the player is not colliding with anything).
We don’t want to move to \(P’\) if it collides with anything. Furthermore, we don’t want to move to \(P’\) if we collide with anything on the way there:
So far we’ve been talking about points (\(P\) and \(P’\)), but what complicates things are the bounding boxes around them. Can we do something to remove the boxes from the equation?
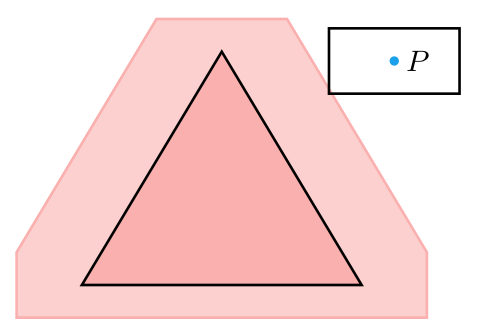
Let’s look at the set of points where \(P’\) collides with our collision volume:
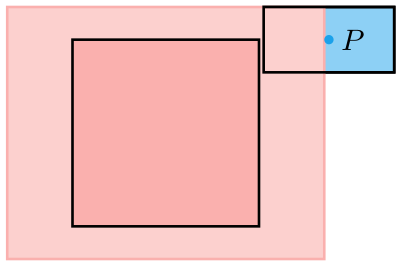
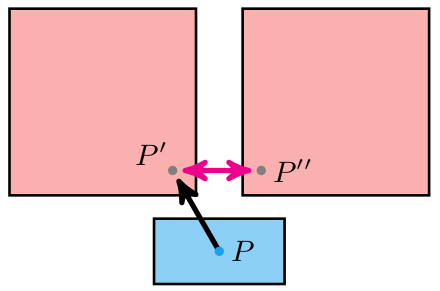
We can change our strategy to simply test \(P’\), a single point, against this larger collision volume. By using it, we remove the complexity of the player’s bounding rectangle, and instead get to work directly with point-in-shape tests.
When checking for a collision, we just have to check whether the ray segment \(P\rightarrow P’\) intersects with the extended volumes, and if it does, only move the player up to the earliest intersection.
If we have multiple collision bodies, this approach will ensure that we stop at the right location:
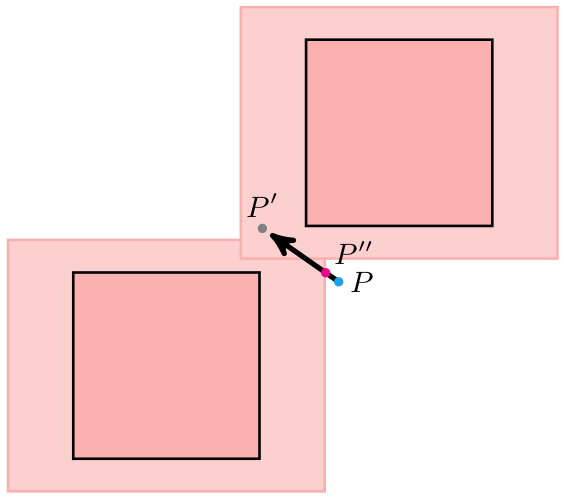
So we are now working with extended volumes. These are obtained by using the Minkowski sum of a collision body with the player’s collision volume. The idea is quite general, and works for arbitrary polygons:
Computing the Minkowski sum of two polygons is actually pretty straightforward:
// Compute the Minkowski sum of two convex polygons P and Q, whose
// vertices are assumed to be in CCW order.
vector<Vec2i> MinkowskiSum(const vector<Vec2i>& P, const vector<Vec2i>& Q) {
// Vertices (a,b) are a < b if a.y < b.y || (a.y == b.y && a.x < b.x)
size_t i_lowest = GetLowestVertexIndex(P);
size_t j_lowest = GetLowestVertexIndex(Q);
std::vector<Vec2i> retval;
size_t i = 0, j = 0;
while (i < P.size() || j < Q.size()) {
// Get p and q via cyclic coordinates
// This uses mod to allow to indices to wrap around
const Vec2i& p = GetCyclicVertex(P, i_lowest + i);
const Vec2i& q = GetCyclicVertex(Q, j_lowest + j);
const Vec2i& p_next = GetCyclicVertex(P, i_lowest + i + 1);
const Vec2i& q_next = GetCyclicVertex(Q, j_lowest + j + 1);
// Append p + q
retval.push_back(p + q);
// Use the cross product to gage polar angle.
// This implementation works on integers to avoid floating point
// precision issues. I just convert floats say, in meters, to
// integers by multiplying by 1000 first so we maintain 3 digits
// of precision.
long long cross = Cross(p_next - p, q_next - q);
if (cross >= 0 && i < P.size()) {
i++;
}
if (cross <= 0 && j < Q.size()) {
j++;
}
}
return retval;
}This post isn’t really about how the Minkowski sum works, so I won’t go too deep into it, but you basically store your polygon vertices in a counter clockwise order, start with a vertex on each polygon that is furthest in a particular direction, and then rotate that furthest direction around in a circle, always moving an index (or both if the directions match) to keep your indices matching that furthest direction.
Sliding and Rolling around Corners
Before we get too deep, let’s quickly cover how to slide along the collision face. Our code above was zeroing out the player’s velocity every time we hit a face. What we want to do instead is zero out the velocity into the face. That is, remove the component of the velocity that points into the face.
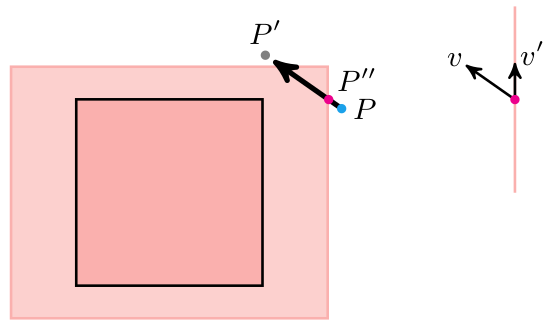
If we know the face unit normal vector \(u\), then we just project our velocity \(v\) into the direction perpendicular to \(u\).
Because running into things slows us down, we typically then multiply our resulting speed vector by a friction coefficient to mimic sliding friction.
// Lose all velocity into the face.
// This results in the vector along the face.
player_vel_ = VectorProjection(player_vel_, v_face);
player_vel_ *= player_friction_slide_; // sliding frictionTo roll around edges we can just trade out our rectangular player collision volume for something rounder. Ideally we’d use a circle, but a circle is not a polygon, so the Minkowski sum would result in a more awkward shape with circular segments. We can do that, but its hard.
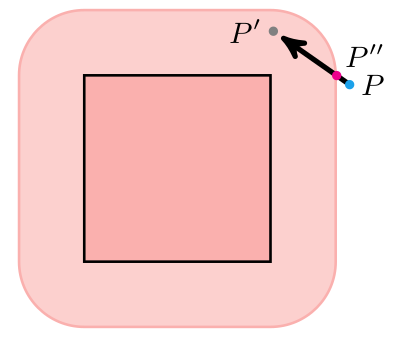
We can instead approximate a circle with a polygon. I’m just going to use a diamond for now, which will give us some rolling-like behavior around box corners.
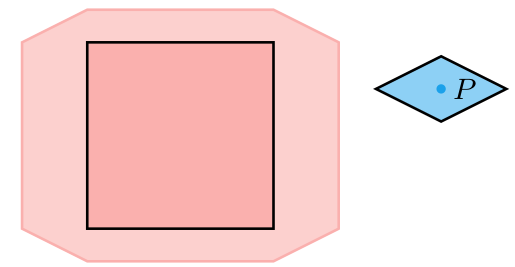
Thinking in Triangles
Now that we took that brief aside, let’s think again about what this Minkowski sum stuff means for the code we prototyped. We could maintain a list of these inflated collision objects and check our points against them every time step. That’s a bit better before, because we’re primarily doing point-in-polygon checks rather than polygon-polygon intersection, but it is still rather complicated, and we want to avoid having to repeatedly iterate over all objects in our level.
I had a big aha! moment that motivated this entire project, which elegantly avoids this list-of-objects problem and ties in nicely with a previous blog post.
What if we build a triangulation of our level that has edges everywhere the inflated collision polygons have edges, and we then mark all triangles inside said polygons as solid. Then all we have to do is keep track of the player’s position and which triangle they are currently in. Any time the player moves, we just check to see if they pass across any of the faces of their current triangle, and if they cross into a solid triangle, we instead move them up to the face.
TLDR: 2D player movement on a constrained Delaunay mesh with solid cells for Minkowksi-summed collision volumes.
To illustrate, here is the Mystic Dave screenshot with some inflated collision volumes:

And here is a constrained triangulation on that, with solid triangles filled in:

And here it all is in action:

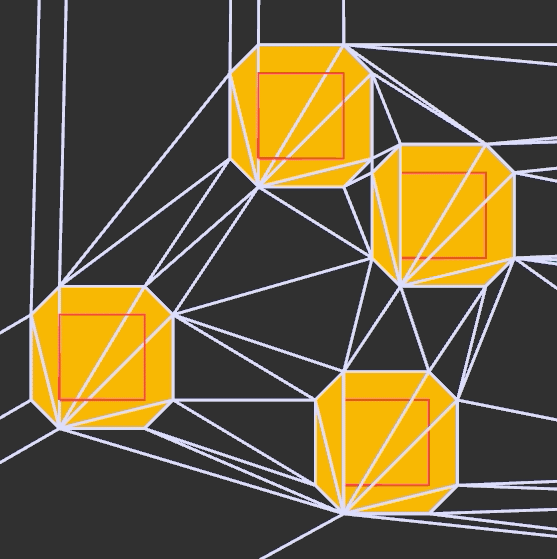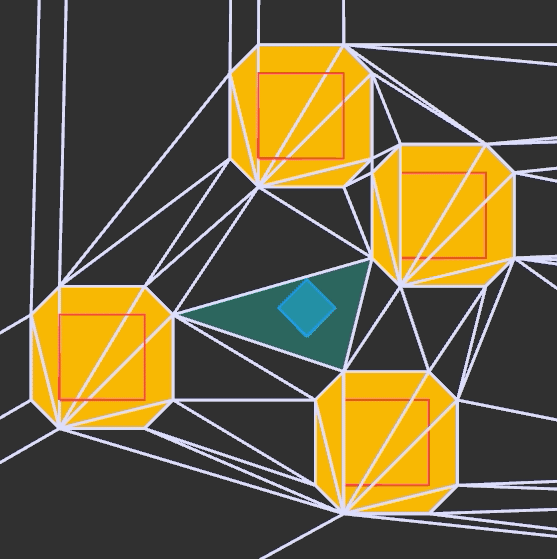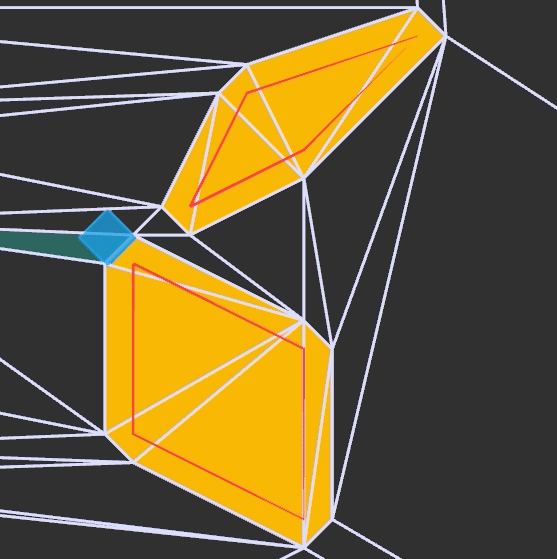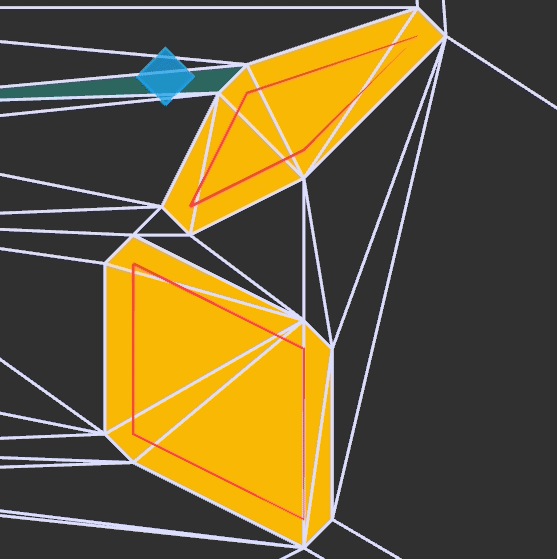
We see the static collision geometry in red, the player’s collision volume in blue, and the inflated collision volumes in yellow. We render the constrained Delaunay triangulation, which has edges at the sides of all of the inflated collision volumes. For player movement we simply keep track of the player’s position, the player’s speed, and which triangle they are in (highlighted).
We don’t have to limit ourselves to tile-centered boxes for this. We don’t even have to limit ourselves to tile-aligned boxes:
Player movement now has to track both the player’s position and the triangle that the player is in. We can find the enclosing triangle during initialization, and can use the same techniques covered the Delaunay Triangulation post. I’m going to repeat that section here, since it is so relevant.
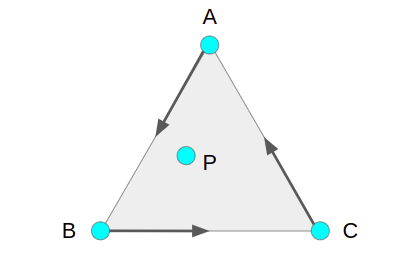
Suppose we start with some random face and extract its vertices A, B, and C. We can tell if a point P is inside ABC by checking whether P is to the left of the ray AB, to the left of the ray BC, and to the left of the ray CA:
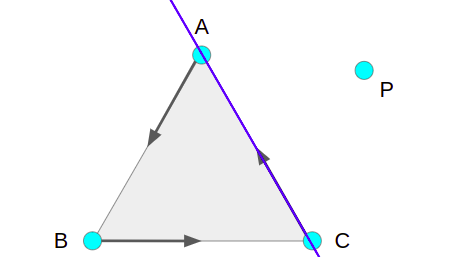
Checking whether P is left of a ray AB is the same as asking whether the triangle ABP has a counter-clockwise ordering. Conveniently, the winding of ABP is given by the determinant of a matrix:
\[\det\left(\begin{bmatrix}A_x & A_y & 1 \\ B_x & B_y & 1 \\ P_x & P_y & 1\end{bmatrix}\right)\]
If this value is positive, then we have right-handed (counter-clockwise) winding. If it is negative, then we have left-handed (clockwise) winding. If it is zero, then our points are colinear.
If our current triangle has positive windings then it encloses our point. If any winding is negative, the we know we can cross over that edge to get closer to our point.
We simply iterate in this manner until we find our enclosing triangle.
Every tick, when we update the player’s position, we run a similar procedure. We similarly are interested in whether the player’s new position has crossed any triangle edges.The basic concept is that, if the new position enters a new triangle, and the new triangle is solid, we need to prevent movement across the edge. If the new position enters a new triangle, and the new triangle is not solid, we can simply move the player and update the enclosing triangle.
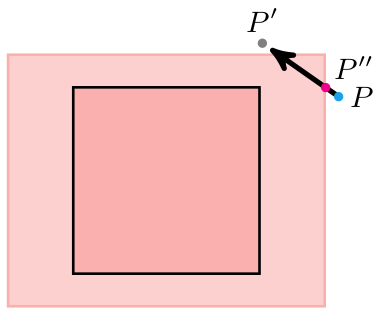
Below we see the simplest case, where the move from P to P’ leads to a new triangle:
If we check the winding of CAP’ and find that it is negative, then we know that we have crossed AC.
There are a few corner cases that make simply accepting the new triangle the wrong thing to do. First off, a single move could traverse multiple triangles:
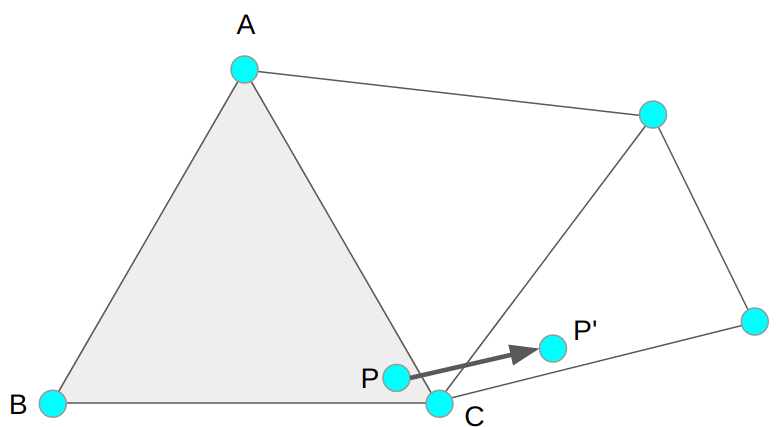
We need to make sure we iterate, and continue to check for edge transitions.
Second, we may cross multiple edges in the first triangle:
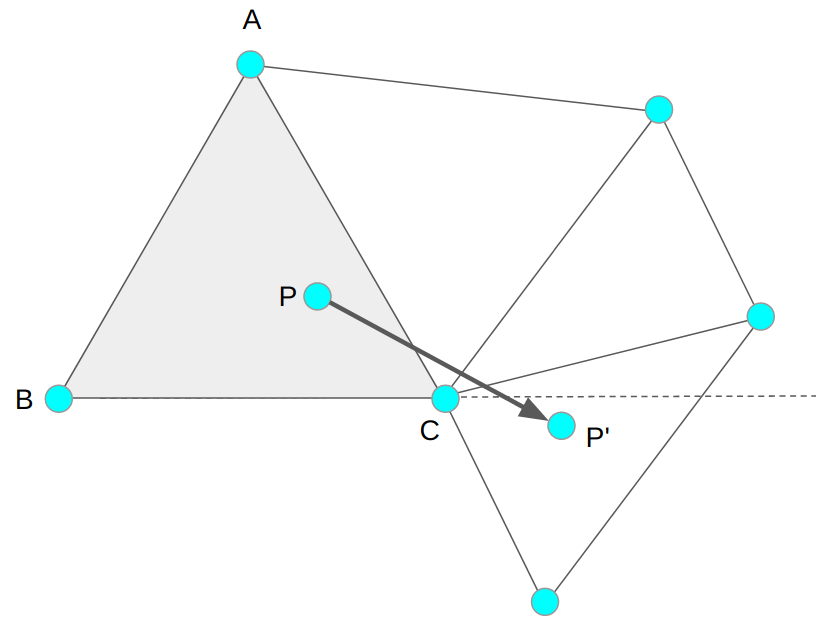
In the above example, the new point P’ is across both the line through BC and the line through CA. The order in which we choose to process these traversals matters, because some intermediate triangles may be solid.
The correct traversal order is to process them in the same order that the ray P -> P’ crosses them. In this case, we first cross CA:
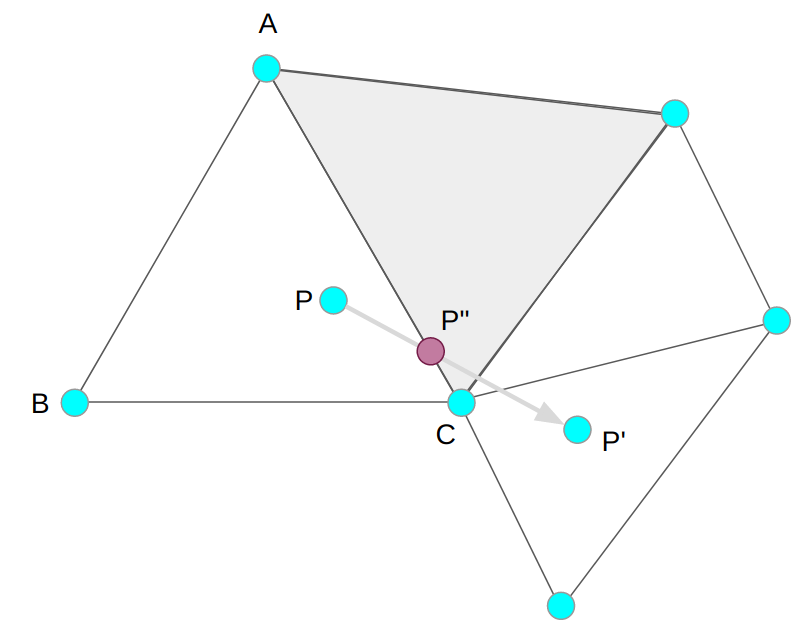
Every time we cross a segment, we find the intersection with the edge and move our player up to that edge. If the new triangle is not solid, we can update our current triangle and iterate again, now with a segment from P” to P’.
If the new triangle is solid, we don’t update our triangle and we process a collision on the colliding face. This means removing all velocity into the face (perpendicular to it) and adding sliding friction along the face (parallel to it). We continue to iterate again, now with a reduced step in our new direction along the edge:
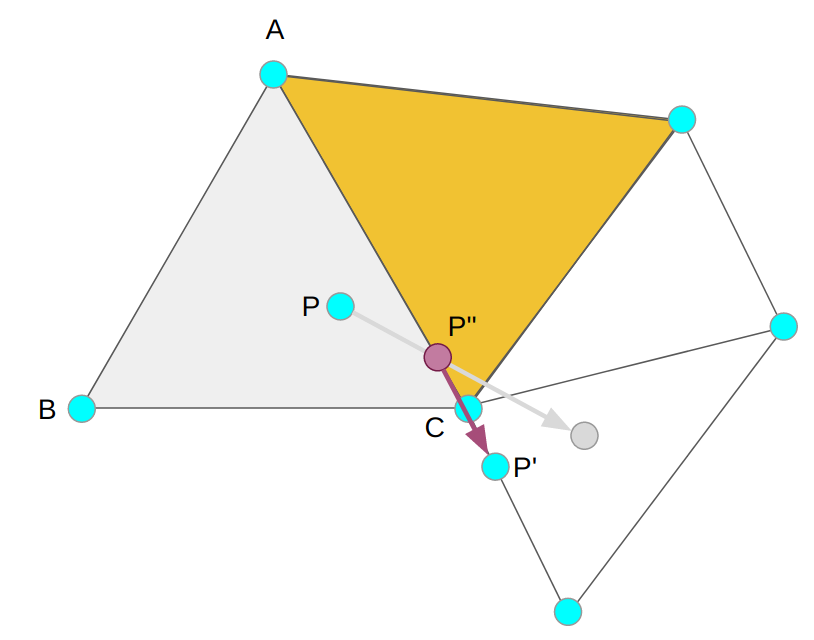
The code structure is thus a while loop that, in each iteration, checks for traversal across all three edges of the enclosing triangle, and retains the earliest collision (if any). If there is a collision, we move the player up to the crossed edge (P”) and potentially handle collision physics or update the enclosing triangle, and iterate again. If there is no collision, then we stay inside our current triangle and are done.
Finding the intersection point for a crossed segment (suppose it is AB) can be done as follows:
\[\begin{aligned}V & = B – A \\ W &= P – A \\ \alpha &= \frac{V \times W }{P’ \times V} \\ P^{\prime\prime} & = P + \alpha (P’ – P) \end{aligned}\]
The interpolant \(\alpha \in [0,1]\) tells us how far we’ve moved toward P’, so is a great way to track which edge we cross first. We first cross the edge with the lowest \(\alpha\).
The code for this is thus:
void UpdatePlayer(Vec2 input_dir, float dt) {
// Update the player's velocity, clamp, etc.
... same as before
// Update the player's position
float dt_remaining = dt;
while (dt_remaining > 0.0f) {
Vec2f player_pos_delta = player_vel_ * dt_remaining;
Vec2f player_pos_next = player_pos_ + player_pos_delta;
// Exit if the step is too small, to avoid math problems.
if (Norm(player_pos_delta) < 1e-4) {
break;
}
// Check to see if we cross over any mesh edges
QuarterEdge* qe_ab = qe_enclosing_triangle_->rot;
QuarterEdge* qe_bc = qe_enclosing_triangle_->next->rot;
QuarterEdge* qe_ca = qe_enclosing_triangle_->next->next->rot;
// Get the vertices
const auto& a = *(qe_ab->vertex);
const auto& b = *(qe_bc->vertex);
const auto& c = *(qe_ca->vertex);
// The fraction of the distance we will move
float interp = 1.0f; // (alpha)
QuarterEdge* qe_new_triangle = nullptr;
Vec2f v_face;
if (GetRightHandedness(a, b, player_pos_next) < -1e-4) {
// We would cross AB
Vec2f v = b - a;
Vec2f w = player_pos_ - a;
float interp_ab = Cross(v, w) / Cross(player_pos_delta, v);
if (interp_ab < interp) {
interp = interp_ab;
qe_new_triangle = qe_ab->rot;
v_face = v;
}
}
if (GetRightHandedness(b, c, player_pos_next) < -1e-4) {
// We would cross BC
Vec2f v = c - b;
Vec2f w = player_pos_ - b;
float interp_bc = Cross(v, w) / Cross(player_pos_delta, v);
if (interp_bc < interp) {
interp = interp_bc;
qe_new_triangle = qe_bc->rot;
v_face = v;
}
}
if (GetRightHandedness(c, a, player_pos_next) < -1e-4) {
// We would cross CA
Vec2f v = a - c;
Vec2f w = player_pos_ - c;
float interp_ca = Cross(v, w) / Cross(player_pos_delta, v);
if (interp_ca < interp) {
interp = interp_ca;
qe_new_triangle = qe_ca->rot;
v_face = v;
}
}
// Move the player
// If we would have crossed any triangle, this merely moves
// the player up to the edge instead
player_pos_ += player_pos_delta * interp;
dt_remaining *= (1.0f - interp);
dt_remaining -= 1e-5; // eps factor for numeric safety
if (qe_new_triangle != nullptr) {
// We would have crossed into a new triangle
if (is_solid(qe_new_triangle)) {
// The new triangle is solid, so do not change triangles
// Process the collision
player_vel_ = VectorProjection(player_vel_, v_face);
player_vel_ *= player_friction_slide_; // sliding friction
} else {
// Accept the new triangle
qe_enclosing_triangle_ = qe_new_triangle;
}
}
}
// Apply air friction
vel_player_ *= kFrictionAir;
}This code block isn’t drastically more complicated than what we had before. We get a lot for it – efficient collision physics against general static objects. There is a bit of repeated code, so you could definitely simplify this even further.
Conclusion
This post revisited the problem of 2D player collision against static geometry. We covered some basics of player movement, including integrating velocity over time, basic collision physics, and basic collision approaches based on geometric primitives. We used the Minkowski sum to inflate collision polygons, thereby changing polygon vs. polygon intersections into cheaper point vs. polygon intersections. We concluded by leveraging constrained Delaunay triangulations for our environment instead, which simplified the collision detection logic down to checking for when we cross enclosing triangle line segments.
Please note that I am not the first to come up with this. It turns out I independently discovered Nav Meshes. I since learned that they are used in motion planning for robotics and in path planning for games (notably, Starcraft II). I assume they are also used for collision physics in games, but I haven’t been able to verify that yet.
I implemented this demo in ROS 2 using C++ 20. This was a deviation from my previous posts, which are mostly created in Julia notebooks. This project had more game-like interactivity to it than I thought a Julia notebook could easily handle (I could be wrong) and I simply felt like I could get up and running faster with ROS 2.
The most complicated part to implement in this whole process turns out to be polygon unions. In order to get the constrained Delaunay triangulation to work, you want to union any overlapping collision polygons together. Polygon unions (and other Boolean operations between polygons, like clipping) is quite complicated. I tried to write my own, but ended up using Clipper2.
I hope you found this process interesting! I was a lot of fun to revisit.