In my previous post, I covered some basic Sokoban search algorithms and some learnings from my digging into YASS (Yet Another Sokoban Solver). I covered the problem representation but glossed over how we determine the pushes available to us in a given board state. In this post, I cover how we calculate that and then conduct into a bunch of little efficiency investigations.

Set of Actions

We are trying to find push-optimal solutions to Sokoban problems. That is, we are trying to get every box on a box in the fewest number of pushes possible. As such, the actions available to us each round are the set of pushes that our player can conduct from their present position:

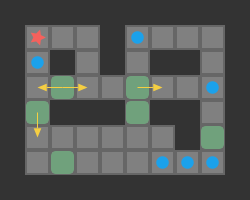
Our Sokoban solver will need to calculate the set of available pushes in every state. As such, we end up calculating the pushes a lot, and the more efficient we are at it, the faster we can conduct our search.

A push is valid if:

• our player can reach a tile adjacent to the block from their current position
• the tile opposite the player, on the other side of the block, is free

As such, player reachability is crucial to the push calculation.

Above we see the tiles reachable from the player’s position (red) and the boxes adjacent to player-reachable tiles. This view is effectively the output of our reachability calculation.

Efficient Reach Calculations

The set of reachable tiles can be found with a simple flood-fill starting from the player’s starting location. We don’t care about the shortest distance, just reachability, so this can be achieved with either a breadth-first or a depth-first traversal:

Naive Reach Calculation

Let’s look at a naive Julia implementation using depth-first traversal:

function calc_reachable_tiles(game::Game, board::Board, □_start::TileIndex)
   min_reachable_tile = □_start
   reachable_tiles = Set{TileIndex}()
   reachable_boxes = Set{TileIndex}()
   to_visit = TileIndex[]
 
   push!(reachable_tiles, □_start)
   push!(to_visit, □_start)
 
   while !isempty(to_visit)
      # pop stack
      □ = pop!(to_visit)
 
      # Examine tile neighbors
      for dir in DIRECTIONS
         ▩ = □ + game.step_fore[dir]
         if ((board[▩] & WALL) == 0) && (▩ ∉ reachable_tiles)
            if ((board[▩] & BOX) == 0)
                push!(to_visit, ▩)
                push!(reachable_tiles, ▩)
                min_reachable_tile = min(min_reachable_tile, □_start)
            else
                push!(reachable_boxes, ▩)
            end
         end
      end
   end
 
   return (reachable_tiles, reachable_boxes, min_reachable_tile)
end

This code is somewhat inefficient, most notably in that it allocates sets for both reachable_tiles and reachable_boxes, which change in size during its execution. (We also compute the minimum reachable tile, for use in state hashing, as explained in the previous post.) Let’s evaluate its runtime on this large puzzle:

Using @btime from BenchmarkTools.jl, we get 15.101 μs (28 allocations: 9.72 KiB). Honestly, 15 microseconds is actually quite good – much better than I expected from a naive implementation. That being said, let’s see if we can do better.

YASS Reach Calculation with Preallocated Memory

I spent a fair amount of time investigating YASS, which was written in Pascal. The Pascal code was structured differently than most of the code bases I’ve worked with. The working memory is declared and allocated at the top of the file in a global space, and is then used throughout. This preallocation makes it incredibly efficient. (As an aside, it was quite difficult to tell where variables were defined, since the naming conventions didn’t make it clear what was declared locally and what was global, and Pascal scoping really threw me into a loop). I feel that a lot of modern programming gets away with assuming we have a lot of memory, and is totally fine with paying the performance cost. However, in tight inner loops like this reach calculation, which might run many hundreds of thousands of times, we care enough about performance to pay special attention.

The Julia performance tips specifically call out paying attention to memory allocations. The previous code allocated 9.72 KiB. Let’s try to knock that down.

We’ll start by defining a struct that holds our preallocated memory. Rather than keeping lists or sets of player-reachable tiles and boxes, we’ll instead store a single flat array of tiles the same length as the board. This representation lets us just flag a given tile as a player-reachable tile or a player-reachable box:

mutable struct ReachableTiles
    # The minimum (top-left) reachable tile. Used as a normalized player position
    min_reachable_tile::TileIndex 
    # Incremented by 2 in each reach calculation
    # The player-reachable tiles have the value 'calc_counter'
    # Tiles with neighboring boxes have the value 'calc_counter' + 1
    # Non-floor tiles are set to typemax(UInt32)
    calc_counter::UInt32
    tiles::Vector{UInt32}
end

This data structure lets us store everything we care about, and does not require clearing between calls (only once we get to wraparound). We just increment a counter and overwrite our memory with every call.

is_reachable(□::Integer, reach::ReachableTiles) = reach.tiles[□] == reach.calc_counter
is_reachable_box(□::Integer, reach::ReachableTiles) = reach.tiles[□] == reach.calc_counter + 1

The reachability calculation from before can now be modified to update our ReachableTiles struct:

function calc_reachable_tiles!(
    reach::ReachableTiles,
    game::Game,
    board::Board,
    □_start::TileIndex,
    stack::Vector{TileIndex}
  )::Int
 
    # The calc counter wraps around when the upper bound is reached
    if reach.calc_counter ≥ typemax(UInt32) - 2
        clear!(reach, board)
    end
 
    reach.calc_counter += 2
    reach.min_reachable_tile = □_start
    reach.tiles[□_start] = reach.calc_counter
    n_reachable_tiles = 1
 
    # depth-first search uses a stack
    stack[1] = □_start
    stack_hi = 1 # index of most recently pushed item
 
    # stack contains items as long as stack_hi > 0
    while stack_hi > 0
        # pop stack
        □ = stack[stack_hi]
        stack_hi -= 1
 
        # Examine tile neighbors
        for dir in DIRECTIONS
            ▩ = □ + game.step_fore[dir]
            if reach.tiles[▩] < reach.calc_counter
                # An unvisited floor tile, possibly with a box
                # (non-floors are typemax ReachabilityCount)
                if (board[▩] & BOX) == 0 # not a box
                    n_reachable_tiles += 1
                    # push the square to the stack
                    stack_hi += 1
                    stack[stack_hi] = ▩
                    reach.tiles[▩] = reach.calc_counter
                    reach.min_reachable_tile = min(▩, reach.min_reachable_tile)
                else
                    # a box
                    reach.tiles[▩] = reach.calc_counter + 1
                end
            end
        end
    end
 
    reach.calculated = true
    return n_reachable_tiles
end

This time, @btime gives us 2.490 μs (2 allocations: 224 bytes), which is about 6x faster and a massive reduction in allocations.

I was particularly pleased by the use of the stack memory passed into this method. Our depth-first traversal has to keep track of tiles that need to be expanded. The code uses a simple vector to store the stack, with just a single index variable stack_hi that points to the most recently pushed tile. We know that we will never have more items in the stack than tiles on our board, so stack can simply be the same length as our board. When we push, we increment stack_hi and place our item there. When we pop, we grab our item from stack[stack_hi] and then decrement. I loved the elegance of this when I discovered it. Nothing magic or anything, just satisfyingly clean and simple.

Avoiding Base.iterate

After memory allocations, the other thing common culprit of inefficient Julia code is a variable with an uncertain / wavering type. At the end of the day, everything ends up as assembly code that has to crunch real bytes in the CPU, so any variable that can be multiple things necessarily has to be treated in multiple ways, resulting in less efficient code.

Julia provides a @code_warntype macro that lets one look at a method to see if anything has a changing type. I ran it on the implementation above and was surprised to see an internal variable with a union type, @_9::Union{Nothing, Tuple{UInt8, UInt8}}.

It turns out that for dir in DIRECTIONS is calling Base.iterate, which returns either a tuple of the first item and initial state or nothing if empty. I was naively thinking that because DIRECTIONS was just 0x00:0x03 that this would be handled more efficiently. Anyways, I was able to avoid this call by using a while loop:

dir = DIR_UP
while dir <= DIR_RIGHT
    ...
    dir += 0x01
end

That change drops us down to 1.989 μs (2 allocations: 224 bytes), which is now about 7.5x faster than the original code. Not bad!

Graph-Based Board Representation

Finally, I wanted to try out a different board representation. The code about stores the board, a 2d grid, as a flat array. To move left we decrement our index, to move right we increment our index, and to move up or down we change by our row length.

I looked into changing the board to only store the non-wall tiles and represent it as a graph. That is, have a flat list of floor tiles and for every tile and every direction, store the index of its neighbor in that direction, or zero otherwise:

struct BoardGraph
    # List of tile values, one for each node
    tiles::Tiles
 
    # Index of the tile neighbor for each tile.
    # A value of 0 means that edge is invalid.
    neighbors::Matrix{TileIndex} # tile index × direction
end

This form has the advantage of a smaller memory footprint. By dropping the wall tiles we can use about half the space. Traversal between tiles should be about as expensive as before.

The reach calculation looks more or less identical. As we’d expect, the performance is close to the same too: 2.314 μs (4 allocations: 256 bytes). There is some slight inefficiency, perhaps because memory lookup is not as predictable, but I don’t really know for sure. Evenly structured grid data is a nice thing!

Pushes

Once we’ve done our reachable tiles calculation, we need to use it to compute our pushes. The naive way is to just iterate over our boxes and append to a vector of pushes:

function get_pushes(game::Game, s::State, reach::ReachableTiles)
    pushes = Push[]
    for (box_number, □) in enumerate(s.boxes)
        if is_reachable_box(□, reach)
            # Get a move for each direction we can get at it from,
            # provided that the opposing side is clear.
            for dir in DIRECTIONS
                □_dest = □ + game.step_fore[dir] # Destination tile
                □_player = □ - game.step_fore[dir] # Side of the player
                # If we can reach the player's pos and the destination is clear.
                if is_reachable(□_player, reach) && ((s.board[□_dest] & (FLOOR+BOX)) == FLOOR)
                    push!(pushes, Push(box_number, dir))
                end
            end
        end
    end
    return pushes
end

We can of course modify this to use preallocated memory. In this case, we pass in a vector pushes. The most pushes we could have is four times the number of boxes. We allocate that much and have the method return the actual number of boxes:

function get_pushes!(pushes::Vector{Push}, game::Game, s::State, reach::ReachableTiles)::Int
    n_pushes = 0
    for (box_number, □) in enumerate(s.boxes)
        if is_reachable_box(□, reach)
            # Get a move for each direction we can get at it from,
            # provided that the opposing side is clear.
            for dir in DIRECTIONS
                □_dest = □ + game.step_fore[dir] # Destination tile
                □_player = □ - game.step_fore[dir] # Side of the player
                # If we can reach the player's pos and the destination is clear.
                if is_reachable(□_player, reach) && ((s.board[□_dest] & (FLOOR+BOX)) == FLOOR)
                    n_pushes += 1
                    pushes[n_pushes] = Push(box_number, dir)
                end
            end
        end
    end
    return n_pushes
end

Easy! This lets us write solver code that looks like this:

n_pushes = get_pushes!(pushes, game, s, reach)
for push_index in 1:n_pushes
    push = pushes[push_index]
    ...
end

An alternative is to do something similar to Base.iterate and generate the next push given the previous push:

"""
Given a push, produces the next valid push, with pushes ordered
by box_index and then by direction.
The first valid push can be obtained by passing in a box index of 1 and direction 0x00.
If there no valid next push, a push with box index 0 is returned.
"""
function get_next_push!(
    game::Game,
    s::State,
    reach::ReachableTiles,
    push::Push = Push(1, 0)
  )
    box_index = push.box_index
    dir = push.dir
    while box_index ≤ length(s.boxes)
        □ = s.boxes[box_index]
        if is_reachable_box(□, reach)
            # Get a move for each direction we can get at it from,
            # provided that the opposing side is clear.
            while dir < N_DIRS
                dir += one(Direction)
                □_dest = game.board_start.neighbors[□, dir]
                □_player = game.board_start.neighbors[□, OPPOSITE_DIRECTION[dir]]
                # If we can reach the player's pos and the destination is clear.
                if □_dest > 0 && 
                   □_player > 0 &&
                   is_reachable(□_player, reach) &&
                   not_set(s.tiles[□_dest], BOX)
                    return Push(box_index, dir)
                end
            end
        end
 
        # Reset
        dir = 0x00
        box_index += one(BoxIndex)
    end
 
    # No next push
    return Push(0, 0)
end

We can then use it as follows, without the need to preallocate a list of pushes:

push = get_next_push!(game, s, reach)
while push.box_index > 0
    ...
    push = get_next_push!(game, s, reach, push)
end

Both this code and the preallocated pushes approach are a little annoying, in a similar what that changing for dir in DIRECTIONS to a while loop is annoying. They uses up more lines than necessary and thus makes the code harder to read. That being said, these approaches are more efficient. Here are solve times using A* with all three methods on Sasquatch 02:

• naive: 17.200 μs
• Preallocated pushes: 16.480 μs
• iterator: 15.049 μs

Conclusion

This post thoroughly covered how to compute the player-reachable tiles and player-reachable boxes for a given Sokoban board. Furthermore, we used this reachability to compute the valid pushes. We need the pushes in every state, so we end up computing both many times during a solver run.

I am surprised to say that my biggest takeaway is actually that premature optimization is the root of all evil. I had started this Sokoban project keen on figuring out how YASS could solve large Sokoban problems as effectively as possible. I spent a lot of time learning about its memory representations and using efficient preallocated memory implementations for the Julia solver.

I would never have guessed that the difference between a naive implementation and an optimized implementation for the reach calculation would merely yield a 7.5x improvement. Furthermore, I would never have thought that the naive implementation for getting the pushes would be basically the same as using a preallocated vector. There are improvements, yes, but it really goes to show that these improvements are really only worth it if you really measure your code and really need that speed boost. The sunk development time and the added code complexity is simply not worth it for a lot of everyday uses.

So far, the search algorithm used has had a far bigger impact on solver performance than memory allocation / code efficiencies. In some ways that makes me happy, as algorithms represent “how we go about something” and the memory allocation / efficiencies are more along the lines of implementation details.

As always, programmers need to use good judgement, and should look at objective data.