Sokoban – the basic block-pushing puzzle – has been on my mind off and on for several years now. Readers of my old blog know that I was working on a block-pushing video game for a short while back in 2012. John Blow, creator of The Witness, later announced that his next new game would draw a lot from Sokoban (In 2017? I don’t remember exactly). Back in 2018, when we were wrapping up Algorithms for Optimization and I started thinking about Algorithms for Decision Making, I had looked up some of the literature on Sokoban and learned about it more earnestly.

At that time I stumbled upon Solving Sokoban by Timo Virkkala, a great Master’s Thesis that covers the basics of the game and the basics used by many solvers. The thesis serves as a great background for search in general, that is, whenever one wants to find the best sequence of deterministic transitions to some goal state. While search problems are not front and center in Algorithms for Decision Making, I did end up writing an appendix chapter on them, and looking back on it see how well comparatively the thesis covers the space.
I started work at Volley Automation in January of 2021, a startup working on fully automated parking garages. I am responsible for the scheduler, which is the centralized planner that orchestrates all garage operations. While the solo pushing of blocks in Sokoban is not quite the same as simultaneously moving multiple robots under trays and having them lift them up, the problems are fairly related. This renewed my interest in Sokoban, and I spent a fair amount of free time looking into solvers.
Early in my investigation, I downloaded an implementation of YASS (Yet Another Sokoban Solver), a 27538-line Pascal program principally written by Brian Damgaard, which I found via the Sokoban wiki. I had heard that this solver could solve the “XSokoban #50” level in under a second, and had found the wiki overview and the code, so felt it was a good place to dive in. After trying to translate the Pascal code into Julia directly, I both determined that the languages are sufficiently different that this was not really possible (Pascal, for example, has a construct similar to a C union, which Julia does not have), and that it also ultimately wasn’t what I wanted to get out of the exercise. I did learn a lot about Pascal and about efficient Sokoban solving from the code base, and ended up translating the overall gist of many algorithms in order to learn how Goal room packing works.
Before I fleshed out YASS’s goal room packing algorithm, I needed a good baseline and a way to verify that my Sokoban game code was correct. As such, I naturally started by writing some of the very basic search algorithms from my search appendix chapter. This post will cover these search algorithms and concretely show how they progressively improve on each other Sokoban problems of increasing complexity. It was really stark to see how the additions in each new algorithm causes order-of-magnitude changes in solver capability. As always, code is here.
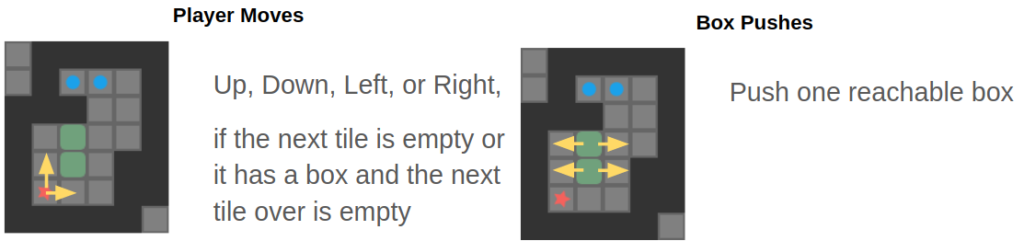
Sokoban Basics
Sokoban is a search problem where a player is on a grid and needs to push some number of boxes to an equal number of goal tiles. The player can move north, south, east, or west, provided that they do not run into a wall or box tile. A player may push a box by moving into its space, provided that the box can move into the next space over. A simple 2-box Sokoban game and solution are shown below:

While the action space is technically the set of legal north/south/east/west player moves, it is more efficient to reason about push moves instead. That is, search algorithms will consider the pushes available from the player’s current position. This simplification yields massive speedups without losing much in terms of practicality. If a push is chosen, we can back out the minimum number of player moves to achieve the push by simply using a shortest-path solver.
A push-optimal solution may not be player move optimal – for example it may alternate between pushing two different boxes that the player has to traverse between – but it is nevertheless well worth reasoning about push moves. Here is the push-move solution for the same simple 2-box problem:

Sokoban is made tricky by the fact that there are deadlocks. We cannot push a box that ends up in a corner, for example. It is not always obvious when one has reached a state from which deadlock is inevitable. A big concern in most Sokoban solvers is figuring out how to efficiently disregard such parts of the search tree.
Problem Representation
A search problem is defined by a state space, an action space, a transition function, and a reward function. Sokoban falls into the category of shortest path problems, which are search problems that simply penalize each step and yield zero reward once a destination state is reached. As such, we are searching for the smallest number of steps to reach a goal state.
The board here has both static and dynamic elements. The presents of walls or goals, for example, does not change as the player moves. This unchanging information, including some precomputed values, are stored in a Game struct:
struct Game
board_height::Int32
board_width::Int32
board::Board # The original board used for solving,
# (which has some precomputation / modification in the tile bit fields)
# Is of length (Width+2)*(Height+2); the extra 2 is for a wall-filled border
start_player_tile::TileIndex
goals::Vector{TileIndex} # The goal tiles do not change
# □ + step_fore[dir] gives the tile one step in the given direction from □
step_fore::SVector{N_DIRS, TileIndex}
# □ + step_left[dir] is the same as □ + step_fore[rot_left(dir)]
step_left::SVector{N_DIRS, TileIndex}
# □ + step_right[dir] is the same as □ + step_fore[rot_right(dir)]
step_right::SVector{N_DIRS, TileIndex}
endwhere TileIndex is just an Int32 index into a flat Board array of tiles. That is,
const TileIndex = Int32 # The index of a tile on the board - i.e. a position on the board const TileValue = UInt32 # The contents of a board square const Board = Vector{TileValue} # Of length (Width+2)*(Height+2)
The 2D board is thus represented as a 1D array of tiles. Each tile is a bit field whose flags can be set to indicate various properties. The basic ones, as you’d expect, are:
const BOX = one(TileValue)<<0 const FLOOR = one(TileValue)<<1 const GOAL = one(TileValue)<<2 const PLAYER = one(TileValue)<<3 const WALL = one(TileValue)<<4
I represented the dynamic state, what we affect as we take our actions, as follows:
mutable struct State
player::TileIndex
boxes::Vector{TileIndex}
board::Board
endYou’ll notice that our dynamic state thus contains all wall and goal locations. This might seem wasteful but ends up being quite useful.
An action is a push:
struct Push
box_number::BoxNumber
dir::Direction
endwhere BoxNumber refers to a unique index for every box assigned at the start. We can use this index to access a specific box in a state’s boxes field.
Taking an action is as simple as:
function move!(s::State, game::Game, a::Push) □ = s.boxes[a.box_number] # where box starts ▩ = □ + game.step_fore[a.dir] # where box ends up s.board[s.player] &= ~PLAYER # Clear the player s.board[□] &= ~BOX # Clear the box s.player = □ # Player ends up where the box is. s.boxes[a.box_number] = ▩ s.board[s.player] |= PLAYER # Add the player s.board[▩] |= BOX # Add the box return s end
Yeah, Julia supports unicode 🙂
Note that this method updates the state rather than producing a new state. It would certainly be possible to make it functional, but then we wouldn’t want to carry around our full board representation. YASS didn’t do this, and I didn’t want to either. That being said, in order to remain efficient we need a way to undo an action. This will let us efficiently backtrack when navigating up and down a search tree.
function unmove!(s::State, game::Game, a::Push) □ = s.boxes[a.box_number] # where box starts ▩ = □ - game.step_fore[a.dir] # where box ends up s.board[s.player] &= ~PLAYER # Clear the player s.board[□] &= ~BOX # Clear the box s.player = ▩ - game.step_fore[a.dir] # Player ends up behind the box. s.boxes[a.box_number] = ▩ s.board[s.player] |= PLAYER # Add the player s.board[▩] |= BOX # Add the box return s end
Finally, we need a way to know when we have reached a goal state. This is when every box is on a goal:
function is_solved(game::Game, s::State) for □ in s.boxes if (game.board[□] & GOAL) == 0 return false end end return true end
The hardest part is computing the set of legal pushes. It isn’t all that hard, but involves a search from the current player position, and I will leave that for a future blog post. Just note that I use a reach struct for that, which will show up in subsequent code blocks.
Depth First Search
I started with depth first search, which is a very basic search algorithm that simply tries all combinations of moves up to a certain depth:
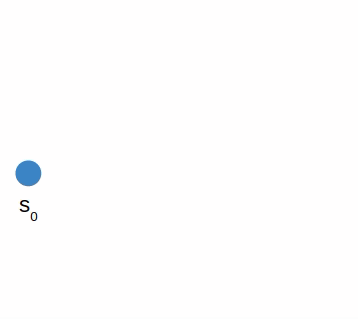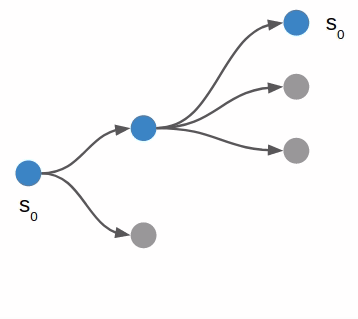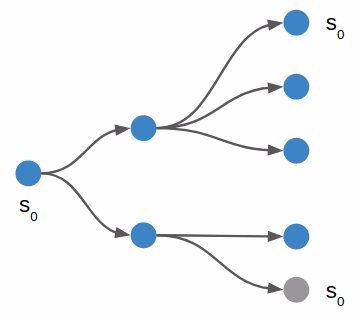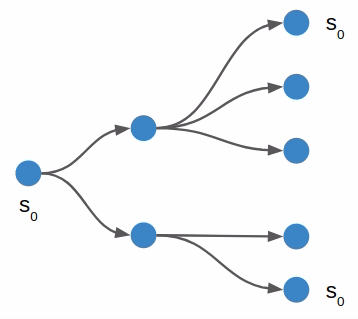
In the book we call this algorithm forward search. The algorithm is fairly straightforward:
struct DepthFirstSearch
d_max::Int
stack::Vector{TileIndex} # Memory used for reachability calcs
end
mutable struct DepthFirstSearchData
solved::Bool
pushes::Vector{Push} # of length d_max
sol_depth::Int # number of pushes in the solution
end
function solve_helper(
dfs::DepthFirstSearch,
data::DepthFirstSearchData,
game::Game,
s::State,
reach::ReachableTiles,
d::Int
)
if is_solved(game, s)
data.solved = true
data.sol_depth = d
return true
end
if d ≥ dfs.d_max
# We exceeded our max depth
return false
end
calc_reachable_tiles!(reach, game, s.board, s.player, dfs.stack)
for push in get_pushes(game, s, reach)
move!(s, game, push)
if solve_helper(dfs, data, game, s, reach, d+1)
data.pushes[d+1] = push
return true
end
unmove!(s, game, push)
end
# Failed to find a solution
return false
end
function solve(dfs::DepthFirstSearch, game::Game, s::State, reach::ReachableTiles)
t_start = time()
data = DepthFirstSearchData(false, Array{Push}(undef, dfs.d_max), 0)
solve_helper(dfs, data, game, s, reach, 0)
return data
endYou’ll notice that I broke the implementation apart into a DepthFirstSearch struct, which contains the solver parameters and memory used while solving, a DepthFirstSearchData struct, which contains the data used while running the search and is returned with the solution, and a recursive solve_helper method that conducts the search. I use this approach for all subsequent methods. (Note that I am simplifying the code a bit too – my original code tracks some additional statistics in DepthFirstSearchData, such as the number of pushes evaluated.)
Depth first search is able to solve the simple problem shown above, and does so fairly quickly:
DFS: solved: true max_depth: 12 n_pushes_evaled: 38 solve_time: 2.193450927734375e-5s sol_depth: 8
While this is good, the 2-box problem is well, rather easy. It struggles with a slightly harder problem:
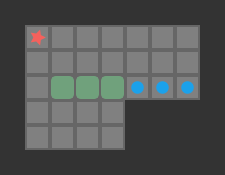
Furthermore, depth first search does not necessarily return a solution with a minimum number of steps. It is perfectly happy to return as soon as a solution is found.
Notice that I do not cover breadth-first search. Unlike depth-first search, breadth-first search is guaranteed to find the shortest path. Why don’t we use that? Doesn’t breadth-first search have the same space complexity as depth-first search, since it is the same algorithm but with a queue instead of a stack?
I am glad you asked. It turns out that DFS and BFS do indeed have the same complexity, assuming that we store the full state in both the stack and the queue. You will notice that this implementation of DFS does not store the full state. Instead, we apply a small state delta (via move!) to advance our state, and then undo the move when we backtrack (via unmove!). This approach is more efficient, especially if the deltas are small and the overall state is large.
Iterative Deepening Depth First Search
We can address the optimality issue by using iterative deepening. This is simply the act of running depth first search multiple times, each time increasing its maximum depth. We know that depth first search will find a solution if d_max is sufficiently large, and so the first run that finds a solution is guaranteed to be a minimum-push solution.
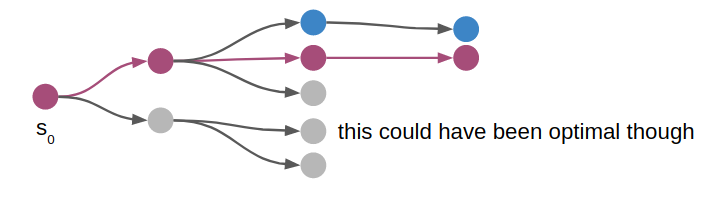
We can re-use depth first search:
struct IterativeDeependingDFS
d_max_limit::Int
stack::Vector{TileIndex}
end
function solve(iddfs::IterativeDeependingDFS, game::Game, s::State, reach::ReachableTiles)
t_start = time()
d_max = 0
solved = false
pushes = Array{Push}(undef, iddfs.d_max_limit)
data = DepthFirstSearchData(false, 0, 0, 0.0, pushes, 0)
clear!(reach, game.board)
while !data.solved && d_max < iddfs.d_max_limit
d_max += 1
dfs = DepthFirstSearch(d_max, iddfs.stack)
solve_helper(dfs, data, game, s, reach, 0)
end
return data
endNow we can solve our 2-box problem in the optimal number of steps:
IDDFS solved: true max_depth: 8 n_pushes_evaled: 1389 solve_time: 0.00043582916259765625s sol_depth: 8
Notice that we evaluated more pushes by doing so, because we exhaustively search all 1-step search trees, all 2-step search trees, all 3-step search trees, …., all 7-step search trees before starting the 8-step search that found a solution. Now, the size of the search tree grows exponentially in depth, so this isn’t a huge cost hit, but nevertheless that explains the larger number for n_pushes_evaled.
Unfortunately, iterative deepening depth first search also chokes on the 3-box problem.
Zobrist Depth First Search
In order to tackle the 3-box problem, we need to avoid exhaustive searches. That is, depth first search will happily push a box left and then re-visit the previous state by pushing the box right again. We can save a lot of effort by not revising board states during a search.
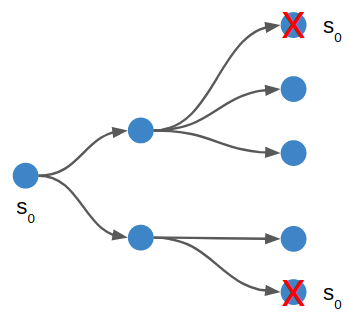
The basic idea here is to use a transposition table to remember which states we have visited. We could simply store every state in that table, and only consider new states in the search if they aren’t already in our table.
Now, recall that our State struct is potentially rather large, and we are mutating it rather than producing a new one with every push. Storing all of those states in a table could quickly become prohibitively expensive. (Debatable, but this is certainly true for very large Sokoban problems).
One alternative to storing the full state is to store a hash value instead. The hash value, commonly a UInt64, takes up far less space. If a candidate state’s hash value is already in our transposition table, then we can be fairly confident that we have already visited it. (We cannot be perfectly confident, of course, because it is possible to get a hash collision, but we can be fairly confident nonetheless. If we’re very worried, we can increase the size of our hash to 128 bits or something).
So to implement depth first search with a transposition table, we need a hash function. I learned a neat method from the YASS entry on the Sokoban wiki about how they do exactly this. First, we observe that the dynamic state that needs to be hashed is the player position and the box positions. Next, we observe that we don’t really care about the player position per-se, but rather which reachable region of the board the player is in. Consider the following game:
The player’s reachable space is:

As far as we are concerned, all of the highlighted tiles have the same legal pushes, so all states are equivalent when conducting a search.
We have to compute the player-reachable tiles anyhow when determining which pushes are legal. As such, we can “normalize” the player position in any state by just using the reachable tile with minimum index in board. If the box positions and this minimum player-reachable tile index match for two states, then we can consider them equivalent.
Finally, we need a way to hash the box positions. This is where Zobrist hashing comes in. This is a hashing technique that is commonly used in games like Sokoban and Chess because we can keep track of the hash by updating it with each move (and un-move), rather than having to recompute it every time from scratch. It works by associating a random unique UInt64 for every tile on the board, and we xor together all of the hash components that correspond to tiles with boxes on them:
function calculate_zobrist_hash(boxes::Vector{TileIndex}, hash_components::Vector{UInt64})::UInt64 result = zero(UInt64) for □ in boxes result ⊻= hash_components[□] end return result end
We can modify Game to store our Zobrist hash components.
The biggest win is that xor’s inverse is another xor. As such, we can modify State to include our current Zobrist hash, and we can modify move and unmove to simply apply and undo the xor:
function move!(s::State, game::Game, a::Push) □ = s.boxes[a.box_number] ▩ = □ + game.step_fore[a.dir] s.board[s.player] &= ~PLAYER s.board[□] &= ~BOX s.zhash ⊻= game.hash_components[□] # Undo the box's hash component s.player = □ s.boxes[a.box_number] = ▩ s.board[s.player] |= PLAYER s.board[▩] |= BOX s.zhash ⊻= game.hash_components[▩] # Add the box's hash component return s end
Easy! Our algorithm is thus:
struct ZobristDFS
d_max::Int
stack::Vector{TileIndex}
# (player normalized pos, box zhash) → d_min
transposition_table::Dict{Tuple{TileIndex, UInt64},Int}
end
mutable struct ZobristDFSData
solved::Bool
pushes::Vector{Push} # of length d_max
sol_depth::Int # number of pushes in the solution
end
function solve_helper(
dfs::ZobristDFS,
data::ZobristDFSData,
game::Game,
s::State,
reach::ReachableTiles,
d::Int
)
if is_solved(game, s)
data.solved = true
data.sol_depth = d
return true
end
if d ≥ dfs.d_max
# We exceeded our max depth
return false
end
calc_reachable_tiles!(reach, game, s.board, s.player, dfs.stack)
# Set the position to the normalized location
s.player = reach.min_reachable_tile
# Exit early if we have seen this state before at this shallow of a depth
ztup = (s.player, s.zhash)
d_seen = get(dfs.transposition_table, ztup, typemax(Int))
if d_seen ≤ d
# Skip!
data.n_pushes_skipped += 1
return false
end
# Store this state hash in our transposition table
dfs.transposition_table[ztup] = d
for push in get_pushes(game, s, reach)
data.n_pushes_evaled += 1
move!(s, game, push)
if solve_helper(dfs, data, game, s, reach, d+1)
data.pushes[d+1] = push
return true
end
unmove!(s, game, push)
end
# Failed to find a solution
return false
end
function solve(dfs::ZobristDFS, game::Game, s::State, reach::ReachableTiles)
empty!(dfs.transposition_table) # Ensure we always start with an empty transposition table
data = ZobristDFSData(false, Array{Push}(undef, dfs.d_max), 0)
solve_helper(dfs, data, game, s, reach, 0)
return data
endThis algorithm performs better on the 2-box problem:
ZOBRIST_DFS solved: true max_depth: 8 n_pushes_evaled: 25 n_pushes_skipped: 4 solve_time: 2.1219253540039062e-5s sol_depth: 8
Note how it only evaluates 25 pushes compared to 1389.
It can easily solve the 3-box problem:
ZOBRIST_DFS solved: true max_depth: 38 n_pushes_evaled: 235522 n_pushes_skipped: 189036 solve_time: 0.0870659351348877s sol_depth: 37
Note how it evaluated 235522 pushes and did not find an optimal solution. We can combine the Zobrist hashing approach with iterative deepening to get an optimal solution:
ITERATIVE_DEEPENING_ZOBRIST_DFS solved: true max_depth: 11 n_pushes_evaled: 174333 n_pushes_skipped: 96738 solve_time: 0.05325913429260254s sol_depth: 11

A* (Best First Search)
For our next improvement, we are going to try to guide our search in the right direction. The previous methods are happy to try all possible ways to push a box, without any intelligence having it tend to push boxes toward a goal, for instance. We can often save a lot of computation by trying things that naively get us closer to our goal.
Where depth-first search expands our frontier in a depth-first order, A* (or best-first search), will expand our frontier in a best-first order. Doesn’t that sound good?
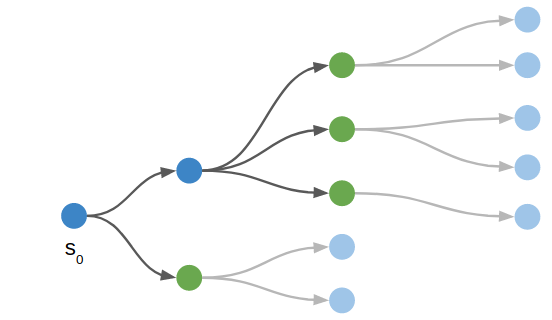
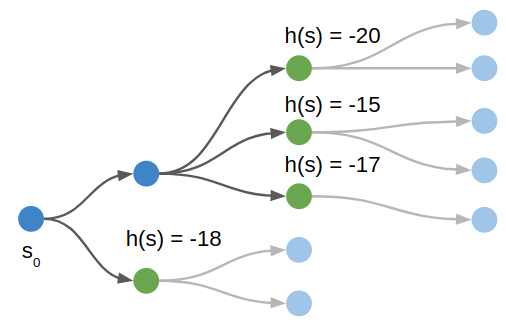
A*, pronounced “A Star”, is a best first search algorithm. It orders its actions according to how good the pushes are, where “goodness” is evaluated by a heuristic function. We are trying to minimize the number of pushes, and as long as this heuristic function gives as a lower bound on the true minimum number of pushes, A* will eventually find an optimal solution.
As with Zobrist depth first search, A* also uses state hashes to know which states have been visited. Unlike Zobrist depth first search, A* maintains a priority queue over which state to try next. This presents a problem, because we don’t store states, but rather apply pushes in order to get from one state to another. Once again, YASS provided a nifty way to do something, this time to efficiently switch from states in one part of the search tree to another.
We will store a search tree for our visited states, but instead of each node storing the full state, we will instead store the push leading to the position. We can get from one state to another by traversing backwards to the states’ common ancestor and then traversing forwards to the destination state. I find the setup to be rather clever:
const PositionIndex = UInt32 mutable struct Position pred::PositionIndex # predecessor index in positions array push::Push # the push leading to this position push_depth::Int32 # search depth lowerbound::Int32 # heuristic cost-to-go on_path::Bool # whether this move is on the active search path end
function set_position!( s::State, game::Game, positions::Vector{Position}, dest_pos_index::PositionIndex, curr_pos_index::PositionIndex, ) # Backtrack from the destination state until we find a common ancestor, # as indicated by `on_path`. We reverse the `pred` pointers as we go # so we can find our way back. pos_index = dest_pos_index next_pos_index = zero(PositionIndex) while (pos_index != 0) && (!positions[pos_index].on_path) temp = positions[pos_index].pred positions[pos_index].pred = next_pos_index next_pos_index = pos_index pos_index = temp end # Backtrack from the source state until we reach the common ancestor. while (curr_pos_index != pos_index) && (curr_pos_index != 0) positions[curr_pos_index].on_path = false unmove!(s, game, positions[curr_pos_index].push) curr_pos_index = positions[curr_pos_index].pred end # Traverse up the tree to the destination state, reversing the pointers again. while next_pos_index != 0 move!(s, game, positions[next_pos_index].push) positions[next_pos_index].on_path = true temp = positions[next_pos_index].pred positions[next_pos_index].pred = curr_pos_index curr_pos_index = next_pos_index next_pos_index = temp end return s end
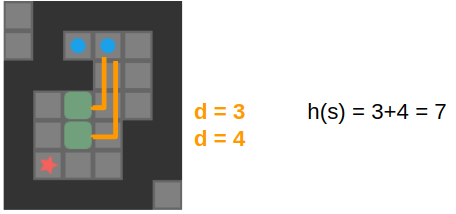
Our heuristic lower bound can take on many forms. One of the simplest is the sum of the distance of each box to the nearest goal, ignoring walls. This is definitely a lower bound, as we cannot possibly hope to require fewer pushes than that. Better lower bounds certainly exist – for example this lower bound does not take into account that each box must go to a different goal.
The lower bound we use is only slightly more fancy – we precompute the minimum number of pushes for each tile to the nearest goal ignoring other boxes, but not ignoring the walls. This allows us to recognize basic deadlock states where a box cannot possibly be moved to a goal, and it gives us a better lower bound when walls separate us from our goals.
The A* implementation is a little more involved than the previous algorithms, but its not too bad:
struct AStar
d_max::Int
n_positions::Int
end
mutable struct AStarData
solved::Bool
max_depth::Int # max depth reached during search
pushes::Vector{Push} # of length d_max
sol_depth::Int # number of pushes in the solution
end
function solve(solver::AStar, game::Game, s::State)
d_max, n_positions = solver.d_max, solver.n_positions
# Allocate memory and recalculate some things
data = AStarData(false, Array{Push}(undef, d_max), 0)
reach = ReachableTiles(length(game.board))
clear!(reach, game.board)
stack = Array{TileIndex}(undef, length(game.board))
pushes = Array{Push}(undef, 4*length(s.boxes))
queue_big = Array{Tuple{TileIndex, TileIndex, Int32}}(undef, length(s.board) * N_DIRS)
distances_by_direction = Array{Int32}(undef, length(s.board), N_DIRS)
dist_to_nearest_goal = zeros(Int32, length(s.board))
calc_push_dist_to_nearest_goal_for_all_squares!(dist_to_nearest_goal, game, s, reach, stack, queue_big, distances_by_direction)
# Calculate reachability and set player min pos
calc_reachable_tiles!(reach, game, s.board, s.player, stack)
move_player!(s, reach.min_reachable_tile)
# Compute the lower bound
simple_lower_bound = calculate_simple_lower_bound(s, dist_to_nearest_goal)
# Allocate a bunch of positions
positions = Array{Position}(undef, n_positions)
for i in 1:length(positions)
positions[i] = Position(
zero(PositionIndex),
Push(0,0),
zero(Int32),
zero(Int32),
false
)
end
# Index of the first free position
# NOTE: For now we don't re-use positions
free_index = one(PositionIndex)
# A priority queue used to order the states that we want to process,
# in order by total cost (push_depth + lowerbound cost-to-go)
to_process = PriorityQueue{PositionIndex, Int32}()
# A dictionary that maps (player pos, zhash) to position index,
# representing the set of processed states
closed_set = Dict{Tuple{TileIndex, UInt64}, PositionIndex}()
# Store an infeasible state in the first index
# We point to this position any time we get an infeasible state
infeasible_state_index = free_index
positions[infeasible_state_index].lowerbound = typemax(Int32)
positions[infeasible_state_index].push_depth = zero(Int32)
free_index += one(PositionIndex)
# Enqueue the root state
current_pos_index = zero(PositionIndex)
enqueue!(to_process, current_pos_index, simple_lower_bound)
closed_set[(s.player, s.zhash)] = current_pos_index
done = false
while !done && !isempty(to_process)
pos_index = dequeue!(to_process)
set_position!(s, game, positions, pos_index, current_pos_index, data)
current_pos_index = pos_index
push_depth = pos_index > 0 ? positions[pos_index].push_depth : zero(Int32)
calc_reachable_tiles!(reach, game, s.board, s.player, stack)
# Iterate over pushes
n_pushes = get_pushes!(pushes, game, s, reach)
for push_index in 1:n_pushes
push = pushes[push_index]
move!(s, game, push)
calc_reachable_tiles!(reach, game, s.board, s.player, stack)
move_player!(s, reach.min_reachable_tile)
# If we have not seen this state before so early, and it isn't an infeasible state
new_pos_index = get(closed_set, (s.player, s.zhash), zero(PositionIndex))
if new_pos_index == 0 || push_depth+1 < positions[new_pos_index].push_depth
lowerbound = calculate_simple_lower_bound(s, dist_to_nearest_goal)
# Check to see if we are done
if lowerbound == 0
# We are done!
done = true
# Back out the solution
data.solved = true
data.sol_depth = push_depth + 1
data.pushes[data.sol_depth] = push
pred = pos_index
while pred > 0
pos = positions[pred]
data.pushes[pos.push_depth] = pos.push
pred = pos.pred
end
break
end
# Enqueue and add to closed set if the lower bound indicates feasibility
if lowerbound != typemax(Int32)
# Add the position
pos′ = positions[free_index]
pos′.pred = pos_index
pos′.push = push
pos′.push_depth = push_depth + 1
pos′.lowerbound = lowerbound
to_process[free_index] = pos′.push_depth + pos′.lowerbound
closed_set[(s.player, s.zhash)] = free_index
free_index += one(PositionIndex)
else
# Store infeasible state with a typemax index
data.n_infeasible_states += 1
closed_set[(s.player, s.zhash)] = infeasible_state_index
end
else
data.n_pushes_skipped += 1
end
unmove!(s, game, push)
end
end
return data
endNotice that unlike the other algorithms, this one allocates a large set of positions for its search tree. If we use more positions than we’ve allocated, the algorithm fails. This added memory complexity is typically worth it though, as we’ll see.
Here is A* on the 3-box problem:
AStar d_max 100 n_positions 500 solved: true total time: 0.0008640289306640625s setup_time: 2.4080276489257812e-5s (2.79%) solving time: 0.0008399486541748047s max_depth: 11 sol_depth: 11 n_pushes_evaled: 1660 n_pushes_skipped: 959 n_infeasible_states: 313 n_positions_used: 388
It found an optimal solution by only evaluating 1,660 pushes, where iterative deepening Zobrist DFS evaluated 174,333. That is a massive win!
A* is able to solve the following 4-box puzzle to depth 38 by only evaluating 5,218 pushes, where iterative deepening Zobrist DFS evaluates 1,324,615:

It turns out that A* can handle a few trickier puzzles:


However, it too fails as things get harder.
Conclusion
There you have it – four basic algorithms that progressively expand our capabilities at automatically solving Sokoban problems. Depth first search conducts a very basic exhaustive search to a maximum depth, iterative deepening allows us to find optimal solutions by progressively increasing our maximum depth, Zobrist hashing allows for an efficient means of managing a transposition table for Sokoban games, and A* with search tree traversal lets us expand the most promising moves.
The YASS codebase had plenty of more gems in it. For example, the author recognized that the lower bound + push depth we use in A* can only increase. As such, if we move a box toward a goal, our overall estimated cost stays the same. But, every state we move from is by definition a minimum-cost state, so the new state is also then minimum cost as well. We can thus save some computation by just continuing to expand from that new state. See, for example, the discussion in “Combining depth-first search with the open-list in A*“.
I’d like to cover the reachability calculation code in a future blog post. I thought it was a really good example of simple and efficient code design, and how the data structures we use influence how other code around it ends up being architected.
Thanks for reading!
Special thanks to Oscar Lindberg for corrective feedback on this post.